初三数学月度检测（苏科版1、3、4章月考试卷）
一、选择题（每题2分，共24分）
1、要使二次根式
有意义，字母
必须满足的条件是（ ）
A、≥1 B、>－1 C、≥－1 D、>1
2、若a<1，化简
的结果是（ ）
A、a－1 B、－a－1 C、1－a D、a+1
3、下列各式属于最简二次根式的是（ ）
A、 B、 C、 D、
4、下列二次根式中与是同类二次根式的是（ ）
A、 B、 C、 D、
5．如图，平形四边形ABCD的周长是28㎝，△ABC的周长是22㎝，则AC的长为（ ）
A．6㎝ B． 12㎝ C．4㎝ D． 8㎝
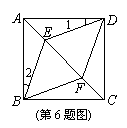
6．如图所示，正方形ABCD中，E、F是对角线AC上两点，连接BE、BF、DE、DF，则添加下列哪一个条件可以判定四边形BEDF是菱形
A、∠1=∠2 B、BE=DF C、∠EDF=60° D、AB=AF
 | |||
 | |||
7、已知
，化简二次根式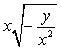
的正确结果为（ ）
A、
B、 
C、
D、
8、已知ax2－5x+1=0是一元二次方程，则不等式a+6>0的解集是（ ）
A、a>－6 B、a>－6且a≠0 C、a<－6 D、a>
9、已知关于x的方程(1) 
(2) 
(3) 
(4) 
(5) 
其中一定是一元二次方程有（ ）
A、(3)(4)(5) B、(1)(3)(4)(5) C、(4)(5) D、(1)(3)(5)
10、一元二次方程
的根的情况是（ ）
A、有一个实数根 B、有两个相等的实数根
C、有两个不相等的实数根 D、没有实数根
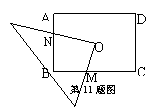
11、如图，O为矩形ABCD的中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC、AB相交，交点分别为M、N．如果AB=4，AD=6，O M=
,ON=
则 与的关系是（ ）
A．
B．
C．
D．
12、若化简
的结果为
，则x的取值范围是（ ）
A、x是任意实数 B、1≤x≤4 C、x≥1 D、x≥4
二、填空（每题2分，共16分）
13、方程
的解为 .
14、已知关于x的一元二次方程
有一个解是0，则m= 。
15、若梯形的面积为12
，高为3
，则此梯形的中位线长为 。
16、如果非零实数n是关于的一元二次方程
的一个根，那么
= 。
17、化简
= 。
18、如图，在△ABC中，点D、E、F分别在BC、AB、AC上，且DE∥AC，DF∥AB。
（1）如果∠BAC=90°，那么四边形AEDF是_____________形；
（2）如果AD是△ABC的角平分线，那么四边形AEDF是_____________形；
（3）如果∠BAC=90°，AD是△ABC的角平分线，那么四边形AEDF是_____________形。
19、某商品经过两次降价，由每件100元调至81元，则平均每次降价的百分率是 。
20、若
，则
=
。
三、计算或解方程（每题4分，共20分）
21． (2－3)×
22． 
（a>0，b>0）
23． 
（配方法） 24 ．
（公式法）
25．
四、计算或证明（本题共12分）
26．证明：两条对角线相等的梯形是等腰梯形。（本题共6分）
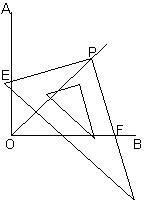
27．（本题共8分）如图，∠AOB=90°，将三角尺的直角顶点落在∠AOB的平分线OC的任意一点P上，使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。
（1）证明PE=PF；（4分）
（2）若OP=10 ，试探索四边形PEOF的面积为定值，并求出这个定值。（4分）
五、应用题（本题共16分）
28．把一根长为80
的绳子剪成两段，并把每一段绳子围成一个正方形。
（1）要使这两个正方形面积之和等于200
，该怎么剪？
（2）这两个正方形面积之和可能等于488吗？（本题共8分）
29．西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价O.1元/千克，每天可多售出40千克.另外，每天的房租等固定成本共24元.该经营户要想每天盈利2O0元，应将每千克小型西瓜的售价降低多少元? （本题共8分）
六.阅读并解答问题。（本题共10分）
30.配方法可以用来解一元二次方程，还可以用它来解决很多问题。因为
，所以
就有个最小值1，即
，只有当
时，才能得到这个式子的最小值1。同样，因为
，所以
有最大值1，即
，只有在时，才能得到这个式子的最大值1。
①当=
时，代数式
有最 （填写大或小）值为
。
②当= 时，代数式
有最 （填写大或小）值为
。
分析：
_____
_____
_____
_____。
③矩形花园的一面靠墙，另外三面的栅栏所围成的总长度是16m，当花园与墙相邻的边长为多少时，花园的面积最大？最大面积是多少？（6分）
 |
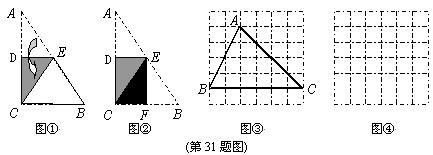
31．（本小题满分10分）操作与探究：
（1）图①是一块直角三角形纸片。将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕。试证明△CBE等腰三角形；
（2）再将图①中的△CBE沿对称轴EF折叠(如图②)。通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合(指无缝无重叠)所成的矩形，我们称这样的两个矩形为“组合矩形”。你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点(各小正方形的顶点)上；
（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)。请你进一步探究，一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件是，一定能折成组合矩形？
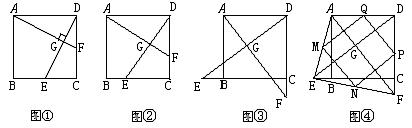
32．（本小题满分12分）如图①，在正方形ABCD中，点E、F分别为边BC、CD的中点，AF、DE相交于点G，则可得结论：①AF=DE，②AF⊥DE。(不需要证明)
(1)如图②，若点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF。则上面的结论①、②是否仍然成立？(请直接回答“成立”或“不成立”)
(2)如图③，若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由。
(3)如图④，在(2)的基础上，连接AE和EF，若点M、N、P、Q分别为AE、EF、FD、AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程。
