期末测试模拟卷(B卷)
一、选择题(共10题,每题2分,共20分.)
1、用幻灯机将一个三角形ABC的面积放大为原来的16倍,下列说法中正确的是( )
A、放大后∠A 、∠B、∠C是原来的16倍; B、放大后周长是原来的4倍
C、放大后对应边长是原来的16倍; D、放大后对应中线长是原来的16倍
2、若2y-7x=0,则x∶y等于 ( )
A、7∶2 B、4∶7 C、2∶7 D、 7∶4
3、如图,A、B、C、D是⊙O上的三点,∠BAC=30°,则∠BOC的大小是 ( )
 A、60° B、45° C、30° D、15°
A、60° B、45° C、30° D、15°
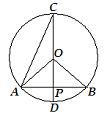 4、如图,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是( )
4、如图,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是( )
A、AB⊥CD B、∠AOB =4∠ACD
C、AD与BD这两条弧相等 D、PO =PD
5、二次函数y=(x-1)2+8的最小值是 ( )
A、-8 B、8 C、-1 D、1
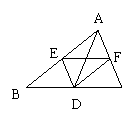 6、如图,点D、E、F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
6、如图,点D、E、F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
A、FD∥AB B、 EF=![]() BC
BC
|
7、函数y=![]() (k≠0)的图象过点(2,-2),则此函数的图象在( )
(k≠0)的图象过点(2,-2),则此函数的图象在( )
A、第一、三象限 B、第三、四象限
C、第一、二象限 D、第二、四象限
8、知二次函数![]() 的图象如图4所示,则下列结论:
的图象如图4所示,则下列结论:
(1)4a+2b+c>0
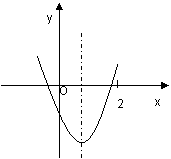 (2)方程
(2)方程![]() 两根之和小于零
两根之和小于零
(3)![]() 随
随![]() 的增大而增大
的增大而增大
(4)一次函数![]() 的图象一定不过第二象限,其中正确的个数是 ( )
的图象一定不过第二象限,其中正确的个数是 ( )
A、 4个 B、 3个 C、2个 D、1个
9、如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=10㎝,则PQ的值为 ( )
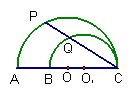 A、5㎝ B、
A、5㎝ B、![]() C、6 D、8㎝
C、6 D、8㎝
10、如图:这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为 ( )
A、![]() 平方米 B、
平方米 B、![]() 平方米 C、
平方米 C、![]() 平方米
D、
平方米
D、![]() 平方米
平方米
 |
二、填空题(共8题,每题3分,共24分.)
11、若![]() ,则
,则![]() =_______________.
=_______________.
12、如图,⊙O的直径CD与弦AB交于点M,添加一个条件 得到M
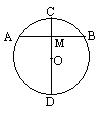 是AB的中点.
是AB的中点.
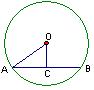 13、在⊙O中,AB为弦,OC⊥AB,垂足为C,若AO=5cm,OC=3cm,则弦AB的长为_______cm。
13、在⊙O中,AB为弦,OC⊥AB,垂足为C,若AO=5cm,OC=3cm,则弦AB的长为_______cm。
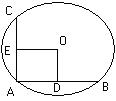 14、如图:在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则⊙O的半径为
cm。
14、如图:在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则⊙O的半径为
cm。
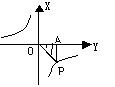 15、如图,P是反比例函数的图象上一点,过P点向x轴作垂线,垂足为A,所得的三角形PAO的面积为3,这个反比例函数的解析是式为
.
15、如图,P是反比例函数的图象上一点,过P点向x轴作垂线,垂足为A,所得的三角形PAO的面积为3,这个反比例函数的解析是式为
.
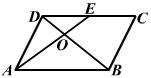 16、如图,在□ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于 cm2.
16、如图,在□ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于 cm2.
17、亮亮想制作一个圆锥模型,这个模型的侧面是用一个半径为9cm,圆心角为240°的扇形铁皮制作的,再用一块圆形铁皮做底。请你帮他计算这块铁皮的半径为 cm。
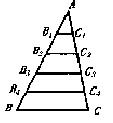 18、如图,在△ABC中,BC=a,B1,B2,B3,B4是AB边的五等分点;C1,C2.C3.C4是AC边的五等分点,则B1C1+B2C2+B3C3+B4C4=__________.
18、如图,在△ABC中,BC=a,B1,B2,B3,B4是AB边的五等分点;C1,C2.C3.C4是AC边的五等分点,则B1C1+B2C2+B3C3+B4C4=__________.
三、解答题(8题,共56分.)
19、如图,在平面直角坐标系中,已知△ABC,点P(1,2).
(1)作△PQR,使△PQR与△ABC相似(不要求写出作法);
(2)在第(1)小题所作的图形中,求△PQR与△ABC的周长比. (6分)
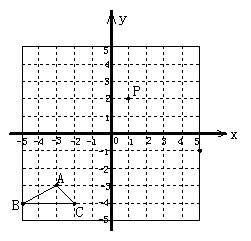
20、如图,⊙O是△ABC的外接圆,已知∠ACO=30°,求∠B的度数. (6分)
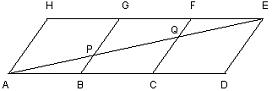
21、如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,若AB=6,求线段BP的长。(6分)
22、反比例函数y=k/x的图象上有一点P(m,n),其坐标是关于t的一元二次方程t2-3t+k=0的两个根,且P到原点的距离为![]()
![]() ,求该反比例函数的解析式。(6分)
,求该反比例函数的解析式。(6分)
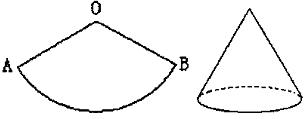
23、如图,扇形OAB的圆心角为120°,半径为6cm.
(1)请用尺规作出此扇形的对称轴(不写作法,保留作图痕迹);
(2)若将此扇形围成一个圆锥的侧面 (不计接缝),求圆锥的底面半径.(6分)
24、如图,抛物线![]() 经过点A(1,0),与y轴交于点B。(7分)
经过点A(1,0),与y轴交于点B。(7分)
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标。

25、(本小题满分9分)
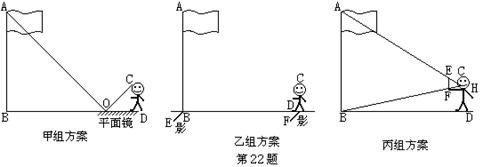
某校八年一班的一节数学活动课安排了测量操场上悬挂国旗的旗杆的高度.甲、乙、丙三个学习小组设计的测量方案如图所示:甲组测得图中BO=60米,OD=3.4米,CD=1.7米;乙组测得图中,CD=1.5米,同一时刻影长FD=0.9米,EB=18米;丙组测得图中,EF∥AB、FH∥BD,BD=90米,EF=0.2米,人的臂长(FH)为0.6米,请你任选一种方案,利用实验数据求出该校旗杆的高度.
26、(本小题满分10分)
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
 |
27、附加题(本小题满分10分)
已知:如图,抛物线![]() 关于
关于![]() 轴对称;抛物线
轴对称;抛物线![]() 关于y轴对称。抛物线
关于y轴对称。抛物线![]() 与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线
与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线![]() 的顶点。HN垂直于x轴,垂足为N,且
的顶点。HN垂直于x轴,垂足为N,且![]()
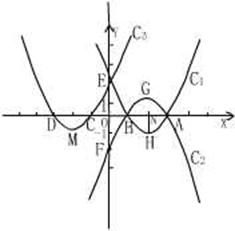 (1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形
;等腰梯形
;平行四边形
;梯形
;(每种特殊四边形只能写一个,写错、多写记0分)
(1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形
;等腰梯形
;平行四边形
;梯形
;(每种特殊四边形只能写一个,写错、多写记0分)
(2)证明其中任意一个特殊四边形;
(3)写出你证明的特殊四边形的性质。
答案:
一、选择题(共10题,每题2分,共20分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | lO |
| 答案 | B | C | A | D | B | D | D | D | B | B |
二、填空题(共8题,每题3分,共24分.)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 |
| CD⊥AB, 等 | 8 |
| Y= | 48 | 6 | 2a |
三、解答题(8题,共56分.)
19、略
20、答:60度
21、答: BP=2
22、解: ∵P(m, n)在反比例函数y=k/x 的图象上.
∴n=k/m , 即 m·n=k
∵m, n是方程 t2-3t+k=0的根, ∴m + n=3
∵P(m,
n)到原点的距离为![]()
∴![]() , 即 m2+n2=13
, 即 m2+n2=13
∵(m +n)2= m2+n2+2 m n , ∴9=13+2k . k= -2
并且当k= -2时, 一元二次方程为t2-3t-2=0有两根.
∴ 反比例函数的解析式为 y= -2/x .
23、(1) 略(2)r=2
24、(1)y=-x2+5x-4;(2)P(0,4)或P(0,![]() )
)
25、解:选择甲组方案计算:
在△ABO和△CDO中,因为∠ABO=∠CDO=90°,∠COD=∠AOB,
所以△ABO∽△CDO.
所以![]() ,所以
,所以![]() ,
,
又BO=60米,OD=3.4米,CD=1.7米,![]()
即该校的旗杆为30米
选择乙组方案计算:
连AE,CF,在△ABE和△CDF中,因为∠ABE=∠CDF=90°,∠AEB=∠CFD,
所以△ABE∽△CDF.所以![]() ,又CD=1.5米,FD=0.9米,EB=18米
,又CD=1.5米,FD=0.9米,EB=18米
所以![]() ,即该校的旗杆为30米
,即该校的旗杆为30米
选择丙组方案计算:
由FH∥BD,可得∠CFH=∠CBD,∠FCH=∠BCD,所以△CFH∽△CBD,![]() ,
,
又EF∥AB,可得∠FEC=∠BAC,∠FCE=∠BCA,△CFE∽△CBA,![]() ,
,
所以![]()
又BD=90米,EF=0.2米,FH=0.6米,![]() ,
,
即该校的旗杆为30米.
26、解:(1)证∠APE=∠ADQ,∠AEP=∠AQD.
(2)注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF=![]() ,
,
得S△PEF=![]() =
=![]() . ∴当
. ∴当![]() ,即P是AD的中点时,S△PEF取得最大值
,即P是AD的中点时,S△PEF取得最大值![]() .
.
(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
27、解:(1)菱形:AHBG,EBFC,AFDE
等腰梯形:HGEF,BCMH,AHMD
梯形:DMHC,MHAB
平行四边形:EGFM,AHMC,MHBD,AGDM
(2)在四边形EBFC中,∵![]() 关于y轴对称
关于y轴对称
∴OC=OB
∵![]() 关于x轴对称
关于x轴对称
∴OE=OF
又EF⊥OB
∴EBFC为菱形
(3)菱形的性质有:①四条边相等
②对角线互相垂直平分
③每一条对角线平分一组对角
④对角相等