初三第一次月考（数学）
一、选择题(每题4分,共48分)
1、已知
中,自变量x的取值范围是( )
A、
B、
C、x>3 D、x>-3
2、下列图形中，既是轴对称图形又是中心对称图形的是( )
 |
3、如果两点P1(1，y1)和P2(2，y2)在反比例函数
的图象上，那么（ ）
A、y2＜y1＜0 B、y1＜y2＜0 C、y2＞y1＞0 D、y1＞y2＞0
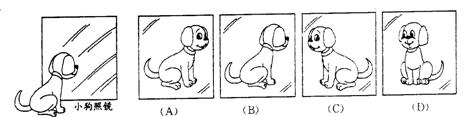4、一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时，它所看到的全身像是( )
5、实验表明，人体内某种细胞的形状可近似地看作球，它的直径约为0.m，则这个数用科学记数法表示是（ ）
A、
B、
C、
D、
6、如图，已知A、B、C是⊙O上的三点，若∠ACB=44°，则∠AOB的度数为（ ）．
A、44° B、46° C、68° D、88°
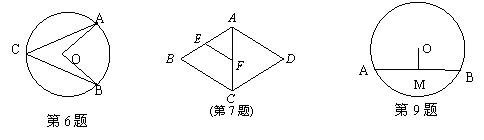
7、如图，在菱形ABCD中，E，F分别是AB，AC的中点，如果EF=2，那么菱形ABCD的周长是（ ）
A、4 B、8 C、12 D、16
8、点A(1,2)向右平移2个单位得到对应点A′,则点A′的坐标是( )
A、(1，4) B、(1，0) C、(-l，2) D、(3，2)
9、如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是（ ）
A、4 B、6 C、7 D、8
10、从A、B、C、D四人中用抽签的方法任选2人去观摩其它班的班队活动，选中A的概率为（ ）
A、
B、
C、
D、
11、下列命题是真命题的是（ ）
A、圆周角等于圆心角的一半 B、等弧所对的圆周角相等
C、平分弦的直径必平分这条弦所对的弧 D、相等的圆心角所对的弧相等
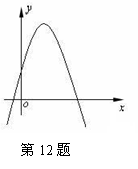12、二次函数
的图象如图所示，则下列结论：
①
＞0； ②
＞0； ③
＞0，其中正确的个数是( )
A、0个 B、1个 C、2个 D、3个
二、填空题(每题5分,共30分)
13、分解因式2x2－18 = _______________.
14、已知反比例函数y＝的图象经过点(1，2)，则k的值是_________。
15、试写出图象位于第二象限与第四象限的一个反比例函数解析式________________.
16、小刚中午放学回家自己煮面条吃，有下面几道工序：①洗锅盛水2分钟；②洗菜3分钟；③准备面条及佐料2分钟；④用锅把水烧开7分钟；⑤用烧开的水煮面条和菜要3分钟，以上各道工序，除④外，一次只能进行一道工序，小刚要将面条煮好，最少用________分钟．
17、杉杉打火机厂生产某种型号的打火机，每只的成本为2元，毛利率为25%。工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，则这种打火机每只的成本降低了_________元(精确到0.01元。毛利率＝)
18、如图，三个单位正方形（即边长为1的正方形）组成“品字形”图形，则能覆盖这个图形的最小圆的面积为__________。
三、解答题(共72分)
19、（本题8分）计算：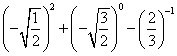
20、（本题8分）解方程：
21、（本题8分）要了解某地区八年级学生的身高情况，从中随机抽取150名学生的身高作为一个样本，身高均在141cm～175cm之间（取整数厘米），整理后分成7组，绘制出频数分布直方图(不完整)．根据图中提供的信息，解答下列问题：
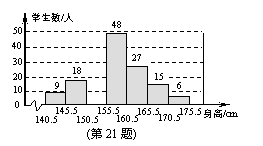(1)补全频数分布直方图；
(2)抽取的样本中，学生身高的中位数在哪个小组?
(3)该地区共有3000名八年级学生，估计其中身高不低于161cm的人数．
22、（本题9分）如图，有一圆形花坛，先要求将它三等分，以便在上面种植不同品种的花。请你设计三种不同的方案。在下面的圆中画出示意图，并请注上必要的说明。（画图工具不限）
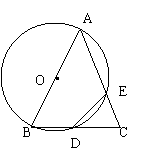23、（本题12分）如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于点E，连接DE，请你找出与线段BD相等的线段，并说明理由。
24、(本题13分)如图，在△ABC中，已知AB＝BC＝CA＝4cm，AD⊥BC于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点Q沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x(s)。
⑴、求x为何值时，PQ⊥AC；
⑵、设△PQD的面积为y(cm2)，当0＜x＜2时，求y与x的函数关系式；
⑶、当0＜x＜2时，求证：AD平分△PQD的面积；
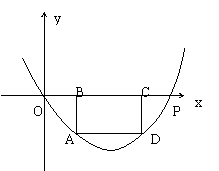25、（本题14分）如图所示，在平面指教坐标系中，抛物线的顶点M到x轴的距离是4，抛物线与x轴相交于O、P两点，OP=4；
（1）请写出P、M两点的坐标，并写出这条抛物线的解析式；
（2）设点A是抛物线上位于O、M之间的一个动点，过A作x轴的平行线，交抛物线于另一点D，作AB⊥x轴于B，DC⊥x轴于C.
①当BC=1时，求矩形ABCD的周长L；
②试问矩形ABCD的周长L是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由.
（3）连接OM、PM，则△PMO为等腰三角形，请判断在抛物线上是否存在点Q（除点P外），使得△OMQ也是等腰三角形，简要说明你的理由（不必求出点Q的坐标）。