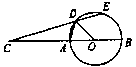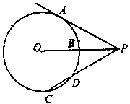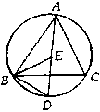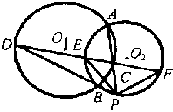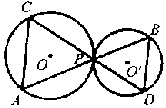| 初三几何---圆 |
| 一.选择题 (本大题共 20 分) |
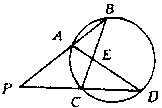
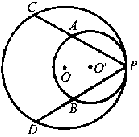
| 1. 如图，自圆外一点P引两条割线PAB和PCD, 连结AD、BC相交于E，则下列各式中成立的是（ ）。
(A) PA·AB=PC·PD (B) AE·BE=CE·DE (C) PB·AB=PD·CD (D) PA·BC=PC·AD |
| 2. 圆内接正四边形的面积与同圆的面积之比为（ ）。 (A)√2:π (B)2:π (C) |
| 3. 两圆的半径分别为12和 4，外公切线长为 15，则两圆的位置关系是( ) (A)内切 (B)相交 (C)外切 (D)外离 |
| 4. 两圆的半径是方程2x2-10x+3=0的两根，两圆外切时，圆心距为( ) (A)4 (B)5 (C)6 (D) |
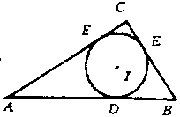
| 5. 如图，⊙I 是RT△ABC 的内切圆, 切点为D、E、F, 如果AF、BE的长是方程 x2-13x+30=0 的两根, 则SΔABC的值是（ ）。
(A) 24 (B) 30 (C) 60 (D) 以上都不是 |
| 6. 同圆的内接正三角形与正六边形的边长之比为（ ）。 (A) 1:2 (B) 1:1 (C)√3:1 (D) 2:1 |
| 7. 一圆锥的母线长恰好等于它的底面直径，若轴截面的面积为 √3 ，则圆锥的侧面积为（ ）。 (A) 12π (B) 4.5π (C) 3π (D) 2π |
| 8. 等边三角形的边长为a，那么它的外接圆的直径是（ ）。 (A) |
| 9. 在矩形ABCD中, AB=5cm, AD=2cn,以直线AB为轴旋转一周所得圆柱的侧面积为（ ）。 (A) 70πcm2 (B) 10πcm2 (C ) 28πcm2 (D)20πcm2 |
| 10. 两圆的内公切线长为3,半径分别为2√3 和√3 ，则内公切线与连心线的夹角为( ). (A)30º (B)45º (C)60º (D)90º |
| 二.填空题 (本大题共 30 分) |
| 1. 两圆的半径为10和3，当两圆外切时，圆心距是 ；当两圆内切时，圆心距是 ；当两圆相交时，圆心距在 和 之间。 |
| 2. 两圆内切时，圆心距为3，其中一个圆半径为8，则另一个圆的半径为 . |
| 3. 扇形的面积为 |
| 4. 两圆半径为4和6，圆心距为20，则内公切线长为 ，两条公切线所夹的角＝ 。 |
| 5. ⊙O1 与⊙O2外切，半径分别为2+√3 和 2-√3 ，则外公切线与连心线的夹角为 ，外公切线长为 。 |
| 6. 等腰梯形ABCD外切于圆，且中位线MN的长是12cm，则梯形ABCD的周长是 。 |
| 7. 半径为2, 圆心角为60°的弓形的面积为 。 |
| 8. 在半径为r的圆中，60º的弧所对的弦长是 ，弦心距是 ，弧长是 。 |
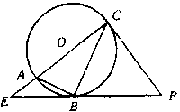
| 9. 如图，AC是⊙O的直径，∠ACB=25° ，PB、PC是⊙O的切线，C、B为切点，则∠E= 。
|
| 10. 120º的圆周角所对的弦长为 4√3 ，那么该圆的直径为 。 |
| 11. 经过 ⊙O内一点P的最大弦长为10cm, 最短弦长为8cm，则OP= 。 |
| 12. 如图，AB是⊙O的直径,延长ED，交BA的延长线与点C，如果∠AOD=50°,AD=DE,那么
|
| 13. 已知AB、 CD为⊙O的两条直径，弦CE//AB , |
| 14. PA、PB 切⊙O于A、B两点，PO交AB于点E，交 |
| 15. 如图，PA切⊙O于点A，PO交⊙O于点B，PDC为割线，如果PB=OB=6，DC=3，那么PA= ，PC= 。
|
| 三.判断题 (本大题共 10 分) |
| 1. 如果一圆的两条切线互相平行那么两切点的连线段是圆的直径。 （ ） |
| 2. 弦切角的度数等于它所夹弧的度数。 （ ） |
| 3. 有外接圆也有内切圆的多边形是正多边形。 （ ） |
| 4. 正多边形一定是中心对称图形。 （ ） |
| 5. 正方形的四个顶点一定在同一个圆上。 （ ） |
| 四.解答题 (本大题共 40 分) |
| 1. 已知扇形的周长为30，面积为56，求扇形的半径的长。 |
| 2. 已知：如图，AB、CD是 ⊙O的直径，弦AE//CD。求证：BD=DE
|
| 3. 已知：如图， ⊙O1与⊙O2交于A、B两点，P是 ⊙O2上一点，PA、PB分别交⊙O1 于C、D，直线CD交于E、F，求证：PE=PF
|
| 4. 已知：如图，⊙O和⊙O＇外切于P，过P作两条直线AB与CD，分别交⊙O于A、C，交⊙O＇于B、D。求证：AC//BD，
|
| 5. 已知：EF是△ABC的中位线,AD⊥BC于D, 交EF于N点，若EF=AD, 求证:以EF为直径的圆必与BC相切 |
| 6. 已知：如图，两圆内切于P，大圆弦PC、PD分别交于小圆于A、B两点， PA=3,AC=2,PB=2,求PD的长。
|
| 7. 如图，在△ABC中，AC=BC,E是内心,AE的延长线交△ABC的外接圆于点D.求证： (1)BE=AE;(2) |
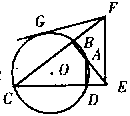
| 8. 如图，ABCD是圆O的内接四边形，BA、CD的延长线交于E，FG圆O于G,且与CB的延长线交于F,若FG=FE.求证：AD//FE。
|
(D)4:π 
(B) 
(C) 
(D) 
,半径为5，则扇形的圆心角为 ，扇形的周长为 。
= ，∠C= 。 
的度数为40°，则∠BOC= 。
于点F，如果∠APB=60°，EF= √3 ，那么OA= ，PA= 。
.
| 初三几何---圆 —— 答案 |
|
|
| 一.选择题 (本大题共 20 分) |
| 1. ：D |
| 2. ：B |
| 3. ：D |
| 4. ：B |
| 5. ：B |
| 6. ：C |
| 7. ：D |
| 8. ：A |
| 9. ：D |
| 10. ：C |
| 二.填空题 (本大题共 30 分) |
| 1. ：13;7;7;13 |
| 2. ：5或11 |
| 3. ： |
| 4. ：10√3 ,60º |
| 5. ：60º,2 |
| 6. ：48cm |
| 7. ： |
| 8. ：r, |
| 9. ：40° |
| 10. ：8 |
| 11. ：3cm |
| 12. ：80°, 15° |
| 13. ：110°或70° |
| 14. ：2√3 , 6 |
| 15. ：6√3 , 12 |
| 三.判断题 (本大题共 10 分) |
| 1. ：对 |
| 2. ：错 |
| 3. ：错 |
| 4. ：错 |
| 5. ：对 |
| 四.解答题 (本大题共 40 分) |
| 1. ：设扇形的半径为R，弧长为L，根据题意得 |
| 2. 因AE//CD,故 |
| 3. ：连结AB、AE，则∠F=∠PAE=∠PAB+∠BAE,∠PAB=∠D,∠BAE=∠BPE.∴∠PEF=∠D+∠BPE=∠PAE=∠F. ∴PE=PF |
| 4. ：过点P作两圆的内公切线 MN ，利用弦切角作为过渡角证得∠A=∠B或∠C=∠D, AC//BD |
| 5. ：提示：证明AD的一半等于EF的一半，由AD⊥BC, 可知EF的中点到BC的距离为EF的一半，故BC与圆相切 |
| 6. ：过点P作两圆的外公切线 MN，证 AB//CD, |
| 7. 提示：(1)由AC=BC得∠BAC=∠ABC，又因为E为△ABC的内心，则 ∠BAE=∠ABE ，所以BE=AE(2)因为 ∠C=∠D，∠BAC=∠BAE+∠EAC=∠BAE+∠ABE=∠∠BED,所以△ABC ∽△EBD， 故 |
| 8. ：由已知条件和切割线定理, 得EF2=FG2=FB·FC， |
, 
, 2R+L=30, 解关于R、L的方程组的R为7或8 
，所以BD=DE
，即 
,又∠BFE=∠EFC，∴△FBE～△FEC，故∠BEF=∠C=∠DAE，则AD//FE