频率与概率练习
一、填空题
1、先后抛掷两枚质地均匀的硬币，两枚硬币都反面朝上的概率为 ；
2、同时掷两个骰子，点数积为6，且其中一个为1点的概率是 ；
3、小红、小芳、小明在一起做游戏时需要确定作游戏的先后顺序，他们约定用“锤子、剪刀、布”的方式确定。请问在一个回合中三个人都出“布”的概率是 ；
4、一个口袋中装有4个白色球，1个红色球，7个黄色球，搅匀后随机从袋中摸出1个球是白色球的概率是 ；
5、中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸，就不能得奖，参与这个游戏的观众有三次翻牌机会（翻过的牌不能再翻）.某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是 ；
6、在一个不透明的袋中装有除颜色外其余都相同的3个小球，其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回，第二次再从袋中摸出一个，那么两次都摸到黄色球的概率是 ；
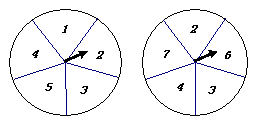
7、图中所示的两个圆盘中,指针落在每一个数上的机会均等,则两个指针同时落在偶数上的概率是 ；
8、小华买了一套科普读物，有上、中、下三册，要整齐的摆放在书架上，有哪几种摆法？其中恰好摆成“上、中、下”顺序的概率是 ；
9、某学校的初一（1）班，有男生20人，女生23人。其中男生有18人住宿，女生有20人住宿。现随机抽一名学生，则：①抽到一名男生的概率是 ；②抽到一名住宿男生的概率是 ；③抽到一名走读女生的概率是 ；
10、一个家庭有3个小孩。（1）这个家庭有3个男孩的概率是 ；（2）这个家庭有2男1女孩的概率是 ；（3）这个家庭至少有1个男孩的概率是 。
11、有两个完全相同的抽屉和3个完全相同的白色球，要求抽屉不能空着．那么第一个抽屉中有2个
球的概率是
12、在一次摸球实验中，一个袋子中有黑色和红色和白色三种颜色除外，其他都相同．若从中任意摸
出一球，记下颜色后再放回去，再摸，若重复这样的实验400次,98次摸出了黄球，则我们可以估计从口袋中随机摸出一球它为黄球的概率是
13、某城镇共有10万人，随机调查2500人，发现每天早上买“城市早报”这种报纸的人为400人，
请问在这个城镇中随便问一个人，他早上买乡“城市早报”的概率是 这家报纸的发行量大约是每天 份．
14、一水塘里有鲤鱼、卿鱼、链鱼共1000尾，一渔民通过多次捕捞实验后发现，鲤鱼、卿鱼出现的
频率是31％和42％，则这个水塘里有鲤鱼 尾，纲鱼尾、缝鱼 尾。
二、选择题：
15、三个人站成一排，通过实验可得，甲站在中间的概率为（ ）
A、
B、
C、
D、
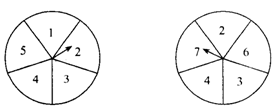
16、如图6所示的两个圆盘中，指针居在每个数上的机会
均等，那么两个指针同时落在偶数上的概率是（ ）
A、
B、
C、
D、
17、小明的衣柜里有两件上衣，一件是长袖的，一件是短袖的；有三条裤子，分别为白色、黄色、蓝色，他任意拿出一件上衣和一条裤子，正好是长袖上衣和白色裤子的概率是（ ）
A、
B、 C、 D、
18、某商店举办有奖销售活动，办法如下：凡购物满100元者得奖券一张，多购多得，每10000张奖券为一个开奖单位，设特等奖1个，一等奖50个，二等奖100个，那么买100元商品的中奖概率应该是（ ）
A、
B、
C、
D、
三、解答题
19、两个布袋中分别装有除颜色外，其他都相同的2个白球，1个黑球，同时从这两个布袋中摸出一个球，请用列表法表示出可能出现的情况，并求出摸出的球颜色相同的概率。
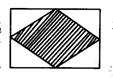20、有一个矩形，将它四边中点连结起来，会得到一个什么图形（阴影部分）？若将一骰子（看做一个点，不考虑它的面积）投到这个矩形中，那么投到阴影部分的概率是多少？你能用计算器模拟这个实验吗？说明实验过程．
21、如果手头没有硬币，但想知道掷一次这种均匀的硬币正面朝上的概率是多少，请问你能用三种不同的方法进行模拟实验吗？请写出实验过程．
22、某小鱼塘放养鱼苗500尾，成活率为80％，成熟后，平均质:VE 1. 5斤以上的鱼为优质鱼，若在一天中随机捞出一条鱼，称出其质量，再放回去，不断重复上面的实验，共捞了50次，有32条鱼的平均质量在1.5斤以上，若优质鱼的利润为2元／斤，则这个小鱼塘在优质鱼上可获利多少元？
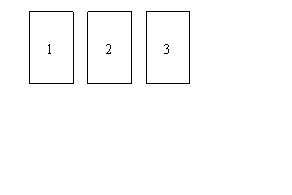
23、从下列两组卡片中各摸一张,用表格求出所摸两张卡片的数字和为5的概率.
|
|
|
24、某种”20选5”的彩票规定:从1—20这20个数字中选择5个(可以重复),如果其中1个与所公布的中奖号码(不妨设为1,2,3,,6,8)相同,可得四等奖,利用计算器模拟实验估计获得四等奖的概率.
25、有两组卡片，第一组三张卡片上都写着A、B、B，第二组五张卡片上都写着A、B、B、D、E。试用列表法求出从每组卡片中各抽取一张，两张都是B的概率。
26、一布袋中有红、黄、白三种颜色的球各一个，它们除颜色外其它都一样。小亮从布袋中摸出一个球后放回去摇匀，再摸出一个球。请你利用列举法（列表或画树状图）分析并求出小亮两次都能摸到白球的概率。
27、将分别标有数字1，2，3 的三张卡片洗匀后，背面朝上放在桌上。
（1） 随机抽取一张，求抽到奇数的概率；
（2） 随机抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，能组成哪些两位数？恰好是32的概率是多少？
28、有一个转盘游戏，转盘平均分成10份（如图），分别标有1、2、……、10这10个数字，转盘上有固定的指针，转动转盘，当转盘停止转动时，指针指向的数字即为转出的数字．两人进行游戏，一人转动转盘，另一人猜数，如果猜的数与转出的数情况相符，则猜数的人获胜，否则转盘的人获胜．猜数的方法为下列三种中的一种：
（1） 猜奇数或偶数；
（2） 猜是3的倍数或不是3的倍数；
（3） 猜大于4的数或不大于4的数．
如果你是猜数的游戏者，为了尽可能取胜，你选哪种猜法？怎样猜？
29、小明和小红正在玩一个游戏：每人掷一个骰子。小明掷的是标准的正方体骰子。而小红用的是均匀的四面体的骰子（标了1，2，3，4）每人掷两次，骰子着地一面是几，就向前走几格。现在两人离开终点目标都是7格。请问谁最有可能先达到终点？请用概率的知识加以分析。
四、学以致用
30、某池塘里养了鱼苗10万条，根据这几年的经验知道，鱼苗成活率为95%，一段时间准备打捞出售，第一网捞出40条，称得平均每条鱼重2.5千克，第二网捞出25条，称的平均每条鱼重2.2千克，第三网捞出35条，称的平均每条鱼重2.8千克，试估计这池塘中鱼的重量。
31、依据闯关游戏规则，请你探究“闯关游戏”的奥秘：
（1）用列表的方法表示有可能的闯关情况；
（2）求出闯关成功的概率.
32、设计一个利用实验法来估计30个人中有2人生日相同的概率的方案。
33、请你为班会活动设计（1）使用一个转盘时中奖率为（2）使用两个转盘中奖率为。
五、公平与否
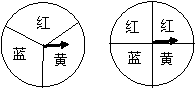34、小英和小丽用两个转盘做“配紫色”游戏，配成紫色小英得1分，否则小丽得1分，这个游戏对双方公平吗？（红色+蓝色=紫色，配成紫色者胜）
35、袋中有黄、白、黑球各1个。任意摸一个后放进去，再摸一次。如果两次摸到的都是同一种颜色，则甲获胜，否则乙获胜。这个游戏对双方公平吗？为什么？
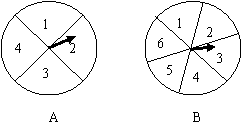
36、如图，有两个可以自由转动的转盘A、B，转盘A被均匀分成4等份，每份标上数字1、2、3、4四个数字；转盘B被均匀分成6等份，每份标上数字1、2、3、4、5、6六个数字。有人为甲乙两人设计了一个游戏，其规则如下：
（1） 同时转动转盘A与B；
（2） 转盘停止后，指针各指向一个数字（如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止），用所指的两个数字作乘积，如果所得的积是偶数，那么甲胜；如果所得的积是奇数，那么乙胜。
你认为这样的规则是否公平？请你说明理由；如果不公平，请你设计一个公平的规则，并说明理由。
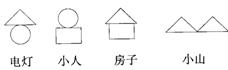
37、小明和小亮用5张同样规格的硬纸片做拼图游戏，正如图1所示，背面完全一样，将它们背面朝上搅匀后，同时抽出两张，规则如下：
当两张硬纸片上的图形可拼成电灯或小人时，小明得1分；当两张硬纸片上的图形可拼成房子或小山时，小亮得1分（如图2）
该游戏规则对双方公平吗？请说明理由；若你认为不公平，如何修改游戏规则才能使游戏对双方都公平？
图 1 图 2
38、某校九年级的初中学生共796名，学生的出生月份统计如下，根据图5中数据回答以下问题：
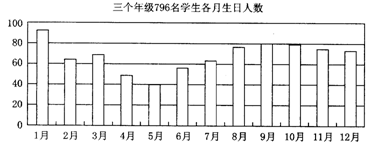
图 1
（1） 出生人数超过60人的月份有哪些？
（2） 出生人数最多的是几月？
（3） 在这些学生中至少有两个人生日在10月5日是不可能的，可能的，还是必然的？
（4） 如果你随机地遇到这些学生中的一位，那么这位学生生日在哪一个月的概率最小？