全旺镇初中九年级月考数学试卷
命题人：李梅荣 2005.12.12
一、选择题(每小题4分)
1．在Rt△ABC中,∠C=90º,AB=5,AC=3,则sinB的值为( ).
2．二次函数
的图象与x轴的交点坐标为( ).
A.(0,0) 、(0,3) B.(0,0) 、(3,0) C.(0,0) 、(-3,0) D.(0,0) 、(0,-3)
3．二次函数
的图象向左平移2个单位长度,得到新图象的函数表达式为( ).
4．某事件发生的概率是
，这意味着（
）
A．每进行三次重复试验该事件一定发生一次；
B．每进行30次重复实验该事件一定发生10次；
C．每进行300次重复实验该事件一定发生100次；
D．以上都不对。
5．袋中共有红、黑两种颜色的球10只，它们除颜色外其他都相同。小明随机地摸了一球，记下颜色后，再放回，摇匀后再摸一球。如此共摸了300次，其中摸到的红球的次数为243次，则袋中约有红球（ ）
A．6只； B．7只； C．8只； D．9只。
6．在同一路灯灯光的照射下，小明的影子比小强的长，则下列说法正确的是（ ）
A、小明比小强高 B、小明比小强矮 C、小明和小强一样高 D、无法判断谁高
7．已知一山坡的坡度
, 则坡角α的度数约为(
).
A.19º B. 71º C.18º D.20º
8．当k>0时,双曲线
与直线 
的交点的个数为( ).
A.0 B.1 C.2 D.3
9．在Rt△ABC中，∠ACB=90º，CD⊥AB于D，BC=3，AC=4，设∠BCD=α，则tanα的值为（ ）
A．
； B．
； C．
； D．
。
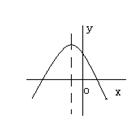
10．已知二次函数
的图象如图所示,则a,b,c满足( ).
A. a<0,b<0,.c>0 B. a<0
,b<0 ,c<0
C. a>0,b<0,c>0 D. a<0,b>0,c>0
二填空题：(每小题5分)
11.将一个均匀的硬币上抛两次，结果为两个正面朝上的概率为___.
12.某蓄电池的电压为36伏,一用电器的限制电流不得超过10A.若以该蓄电池为电源,则该用电器的可变电阻R(Ω)应控制什么范围?________
13. 下图是某天不同时刻直立的竹竿及其影长（规定上北下南）。按编号写出竹竿所在时刻的顺序为 .
14．抛物线
的顶点在x轴上,则k的值为
15.某旅行社组团去旅游,30人起组团,单价每人800元.旅行社对超过30人的团给予优惠,即旅游团每增加一人,每人的单价就降低10元.若设旅游团的人数为x人时该旅行社的营业额为y元,请写出y关于x的函数关系式_______
16. 身高相等的三名同学甲、乙、丙参加风筝比赛，三人放风筝的线长、线与地面夹角如下表（假设风筝线是拉直的），则三人所放的风筝中____最高.
| 同学 | 甲 | 乙 | 丙 |
| 放出风筝线长 | 100米 | 100米 | 90米 |
| 线与地面夹角 | 40度 | 45度 | 60度 |
17.写一个二次函数,满足下列条件： ①其图象的对称轴为直线x=2；②当x>2时,y的值随着x的增大而增大．则这个二次函数可以为___________
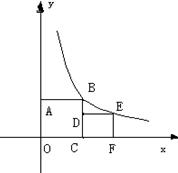
18.如图，四边形OABC、CDEF都是正方形，且B、E在函数
的图象上，点C、F在x轴上，则点F的坐标为_____
三．解答题：
19．（8分）计算: 
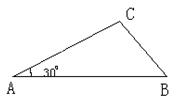
20．(8分)在△ABC中,
求△ABC的面积.
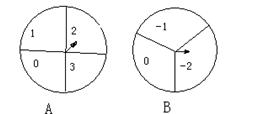
21．有两个可以自由转动的均匀转盘A、B,分别被分成四等份、三等份,并且每份内均标有数字(如图所示).
王扬和刘菲同学用这两个转盘做游戏,游戏规则如下:
① 分别转动转盘A、B;
② 两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份内为止).
③ 如果和为0,王扬获胜;否则刘菲获胜.
⑴用列表法(或树状图)求王扬获胜的概率;(5分)
⑵你认为这个游戏对双方公平吗?请说明理由.(4分)
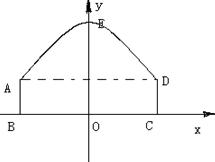
22．如图,隧道的截面由抛物线AED和矩形ABCD构成, 矩形的长BC为8m,宽AB为2m,以BC所在直线为x轴,以线段BC的中垂线为y轴,建立平面直角坐标系,y轴为抛物线的对称轴,顶点E到坐标原点O的距离为6m.
⑴写出A,D,E的坐标,并求抛物线的解析式.(5分)
⑵如果该隧道内设双行道,现有一辆货运卡车高4.2m, 宽2.4m,这辆货运卡车能否通过该隧道?通过计算说明你的结论.(5分)
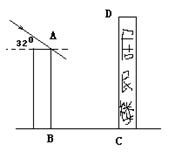
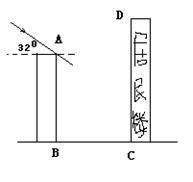
23．(本题10分)如图，某居民小区有一朝向为正南方向的居民楼，该居民楼的一楼是高6米的小区超市，超市以上是居民住房。在该楼的前面15米处要盖一栋高20米的新楼。当冬季正午的阳光与水平线的夹角为32度时。
⑴问超市以上的居民住房采光是否有影响，为什么？
⑵若要使超市采光不受影响，两楼之间应相距多少米？（结果保留整数）
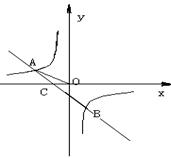24.（本题10分）如图，一次函数
的图象与反比例函数的图象交于A、B两点，已知
点B的坐标为
。
⑴求反比例函数和一次函数的解析式；
⑵根据图象写出一次函数的值小于反比例函数的值的x的取值范围。
25．(本题15分)课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．现初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：
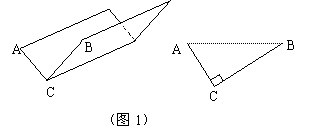
⑴方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米2，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
 |
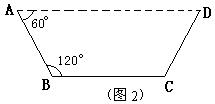
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．
⑵假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）
全旺镇初中九年级第三次月考数学试卷
答题卷
一、选择题（每小题4分，共40分）
| 题号 | １ | ２ | ３ | ４ | ５ | ６ | ７ | ８ | ９ | 1０ |
| 答案 |
二、填空题（每小题5分，共40分）
11._________________________12.________________________
13.________________________ 14._________________________
15.______________________ 16._________________________
17.________________________ 18.__________________________
三、解答题
19. 计算（8分）
20.(本题8分)
解:
21. (本题9分)
22. (本题10分)
23. (本题10分)
24. (本题10分)