2006年初三数学试题 10月份
班级_______姓名_______等级________
一、 请你来选择
1．分式
和
的最简公分母是
（ ）
A.12xyz B.12x2yz C.24xyz D.12x2yz
2．若分式
的值为零，则x的值是
（ ）
A.1 B.－1 C.±1 D.0
3．一个小组有若干人，新年互送贺年卡一张，已知全组共送贺年卡72张，则这个小组共有（ ） A.12人 B.18人 C.9人 D.10人
4．一元二次方程x2－1＝0的根为 （ ）
A.x＝1 B.x＝－1 C.x1＝1，x2＝－1 D.x1＝0，x2＝1
5．制造一种产品，原来每件的成本是100元，由于连续两次降低成本，现在的成本是81元，则平均每次降低成本 （ ）
A.8.5％ B.9％ C.9.5％ D.10％
6．党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年（2001～2020年），要实现这一目标，以十年为单位计算，设每个十年的国民生产总值的增长率都是x，那么x满足的方程为 （ ）
A.（1＋x）2＝2 B. （1＋x）2＝4 C.1＋2x＝2 D.（1＋x）＋2（1＋x）＝4
7. 下列语句正确的有 （ ）
⑴. 相等的圆心角所对的弧相等 ⑵. 平分弦的直径垂直于弦
⑶. 长度相等的弧是等弧 ⑷. 经过圆心的每一条直线都是对称轴
A. 1个 B. 2个 C.3个 D. 4个
8．如果关于x的一元二次方程x2＋px＋q＝0的两根分别为x1＝3，x2＝1，那么这个一元二次方程是 （ ）
A.x2＋3x＋4＝0 B.x2－4x＋3＝0 C.x2＋4x－3＝0 D. x2＋3x－4＝0
9．如图1，已知圆心角∠AOB＝100°，则圆周角∠ACB的度数为 （ ）
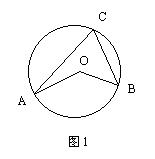A.100 ° B.80° C.50° D.40°
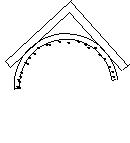
10．用直角钢尺检查某一工件是否恰好是半圆环形，根据图形所
表示的情形，四个工件中哪一个肯定是半圆环形 （ ）
 |  | ||
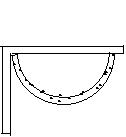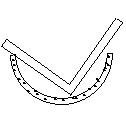A B.
 | |||
 | |||
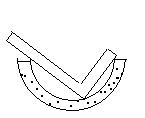C. D .
二、 请你来填空
11．已知a＋
＝3，则a2＋
＝_________。
12．
＋
＝2的解集是________.
13．若关于x的方程x2－ax－3a＝0的一个根是－2，则它的另一个根是______。
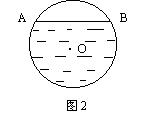
14．如图2，水平放着的圆柱形排水管的截面半径是0.5m，其中水面宽AB为0.6m，则水的最大深度为________。
 |
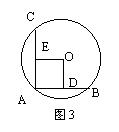
15．如图3，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB，OE⊥AC，垂足分别为D，E，若AC＝2cm，则⊙O的半径为_______cm。
16．若一个三角形的三边长均满足方程x2－6x＋8＝0，则此三角形的周长为_______。
三、请你来探究（6+6+6+8+8+8+12+12）
17．请你先化简，再选一个使原式有意义，而你又喜爱的数代入求值。
－
18、1、解方程
2、解分式方程：
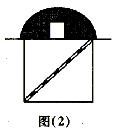
19. 从前有两个醉汉过城门，一个醉汉手里拿着一根竹竿，他横着拿，比城门长8m，竖着
拿比城门长1m，怎么也进不去城门，另一个醉汉夺过这根竹竿，斜着放在城门的两个对角，不多不少正好进了城门（如图2所示）。你知道这根竹竿有多长？
20、阅读材料：为了解方程
，我们可以将
视为一个整体，然后设
，
，则原方程可化为
①
解得
。
当
时，
，
当
∴原方程的解为：
解答问题：（1）仿造上题解方程：
（2）填空：在将原方程化为方程①的过程中，利用了数学_______________法达到降次的目的,体现了________的数学思想.
21.当
时，求
的值。
22．据报道，今年第一季度宁波完成国内生产总值（GDP）354亿元，比杭州少45亿元，宁波和杭州构成了全省经济的第一集群，绍兴（230亿元）和温州（227.5亿元）两城市组成了第二集群，第三集群有台州（194.4亿元）、嘉兴（167.6亿元）、金华（161.7亿元）。
1. 求杭州、宁波、绍兴、温州、台州、嘉兴、金华等七市今年第一季度GDP的平均值（精确到1亿元）；
2. 经预测，宁波市今年第三季度GDP可达到407亿元，那么平均每季度增长的百分率是多少（精确到0.1％）？
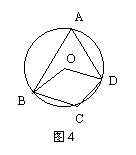
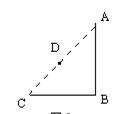
23．如图5，客轮沿折线A－B－C从A出发经B再到C匀速航行，货轮从AC的中点D出发沿某一方向匀速直线航行，将一批物品送达客轮。两船同时起航，并同时到达折线A－B－C上某点E处。已知AB＝BC＝200海里，∠ABC＝90°，客轮速度是货轮速度的2倍。
（1）选择：两船相遇之处E点 （ ）
A.在线段AB上 B.在线段BC上
C.可以在线段AB上，也可以在线段BC上
（2） 求货轮从出发到两船相遇共航行了多少海里？（结果保留根号）
 |
24．某车间利用直角边长为4的等腰直角三角形剩余材料进行产品加工。要在这个等腰直角三角形中剪出一个扇形，使扇形的半径都三角形的边上，且扇形的弧与三角形的其他边相切，
（1） 请在下列正方形网格中设计出尽可能多的形状不同、符合题意设计方案的示意图。
（2） 在你的设计方案中，你认为是方案几最能充分利用材料（扇形面积最大），并求出这个设计方案的扇形面积。
（3） 车间里还有其他边长为4的各种形状不同的等腰三角形，你还能从中找到符合设计要求，且面积不小于第（2）小题中最大面积的三角形吗？若存在，请求出这种三角形所设计的扇形的面积。若不存在，说明理由
