圆—综合测试卷3
一．填空题：
1．ΔOAB中，若OA=OB=2，⊙O半径为1，当∠AOB 时，直线AB与⊙O相切；当∠AOB 时，直线与⊙O相交；当∠AOB 时，直线与⊙O相离。
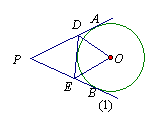
2．如图①，∠APB=500，PA、PB、DE都为⊙O的切线，则∠DOE为 。
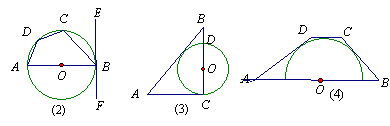
3．如图②，AB是⊙O的直径，直线EF切⊙O于点B，点C、D是⊙O上的点，弦切角∠CBE=500，
，则∠BCD= 。
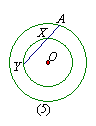
4．如图③，在RtΔABC中，∠C=900，AC=4，BC=3，以BC上一点O为圆心作⊙O与AC、AB都相切。又⊙O与BC的另一个交点为D，则线段BD的长为 。
5． 腰长为10㎝，底边长为6㎝的等腰三角形的内切圆在两腰上的切点间的距离为 。
6．已知三边长为3、4、6的ΔABC的内切圆半径为r，则ΔABC的面积= 。
7． 在⊙O中，弦AB、CD相交于点P，若PA=3，PB=4，CD=9，则以PC、PD的长为根的方程是 。
8．如图⑤，在以O为圆心的两个圆中，A为大圆上的任意一点，过A作小圆的割线AXY，若AX·AY=3，则此圆环的面积为 。
9．已知，已知，AB是⊙O的弦，P是AB上的一点，AB=10㎝，PA=4㎝，OP=5㎝，则⊙O的半径= 。
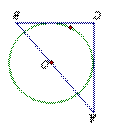
10．如图④，在梯形ABCD中，AB∥CD，半圆O与AD、BC、DC都相切，且圆心O在AB上，⊙O的半径为3，∠A=300，∠B=450，则AB= 。
 | |||||
 |  | ||||
二．选择题
11．已知RtΔABC中，∠C=90
，BC=a、AC=b，以斜边AB上一点O为圆心，作⊙O使⊙O与直角边AC、BC都相切，则⊙O的半径r
A.
B. 
C.
D.
12.等腰直角三角形内切圆半径与外接圆半径的比是（ ）
A
B
C
D
13．如图，已知⊿ABC的内切圆O与各边相切于D、E、F，那么点O是 ⊿DEF的（ ）
A．三条中线的交点 B.三条高的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
14．如图，AB切⊙O于B，割线ACD经过圆心O,若∠BCD=70°则∠A的度数为（ ）
A.20° B.50° C.40° D.80°
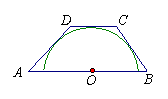15．如图，梯形ABCD中，AB∥CD，AD=3，BC=2，半圆O与AD、DC、BC都相切，且圆O在AB上，AB的长( )
A.6 B.5 C.4 D.3
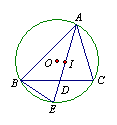16．如图，点I是ΔABC的内心，AI的延长线交BC于点D，交ΔABC的外接圆于E，若IE=4，AE=8，那么DE的长。
A．5 B.4 C.3 D.2
17.已知，AB是⊙O的弦，P是AB上的一点，AB=10㎝，PA=4㎝，OP=5㎝，则⊙O的半径( )。
A.8 B.7 C.6 D.5
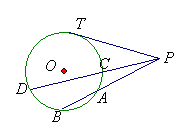18.如图，PT切⊙O于点T，PAB、PCD是割线，弦AB=35㎝，弦CD=50㎝，AC：DB=1：2，求PT的长。
A.60 B.55 C.50 D.45
三．解答题：
1．
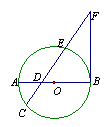如图，AB为⊙O直径，BF⊥AB于B点，割线FEC交AB于D点，AD=2，CD=3，ED=4．求EF的长．
2、如图，A为⊙O外一点，过A作两条直线分别与⊙O交于B、C和D、E点．若BE为⊙O直径，AB=12，DE=30，AD=BC．求∠A的度数和BE的长．
3、如图，在△ABC中，以BC为直径的⊙O交AB于D点，交AC于E点，AD=3，
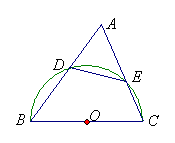S△ADE=S四边形BCED，CE＝
。求：(1)∠A；(2)∠B的正弦值．
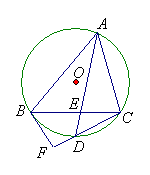4、如图，已知⊙O内接△ABC，D为
中点，AD交BC于E点，过B作⊙O的切线交CD延长线于F点，AE=3，DE=1，BF=
。求CF的长．
四、证明题：
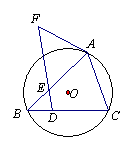1．如图，已知⊙O的内接ΔABC，D在BC上，过D点作AC的平行线交AB于E点，交过A的直线于F点，且BE·AE=DE·EF。求证：AF是⊙O的切线。
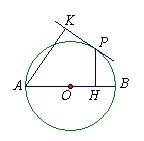2．如图，AB为⊙O直径，自圆上一点P作AB的垂线PH，垂足为H，自点A向过P点的切线作垂线，垂足K。求证：AH＝AK。
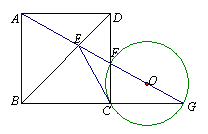
3、如图，由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G，
求证：CE是△CGF的外接圆⊙O的切线。
 |
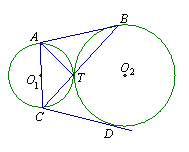
4、如图，⊙O1与⊙O2外切于T，AB为公切线，BT的延长线交⊙O1于点C，CD切⊙O2于点D。
求证：① AC为⊙O1的直径；② AC＝CD。
 |
参考答案
一、填空
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10.
二、选择
1. C 2. C 3. D 4.B 5. B 6. D 7. B 8. A
三、计算
1. 20 2. 
3. 
4. 5
四、证明 （略）