10月份月考试卷（数学）
2006-9
一．选择题(本大题共15小题，每小题3分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的)
1、在函数式
中,自变量
的取值范围是（
）
Ａ.
Ｂ.
Ｃ.
Ｄ.
2、若点P（1－m，m）在第二象限，则下列关系式正确的是 ( )
A．0＜m＜1 B．m＞0 C．m＞1 D．m＜0
3、夏天，一杯开水放在桌子上，杯中水的温度T(℃)随时间t变化的关系的图象是( ).
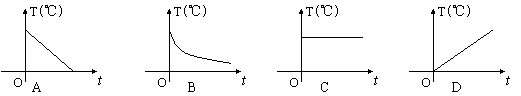
4、下列图形中是轴对称图形的是（ ）
A． B． C． D．
5、抛物线
的顶点坐标是 ( ).
A.(0，-2) B.(-2，0) C.(0，2) D.(2，0)
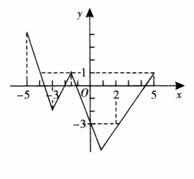
6．如图，是某函数的图象，则下列结论中正确的是 （ ）
A．当
时，的取值是
B．当
时，的近似值是
C．当
时，函数值
最大
D．当
时，随的增大而增大
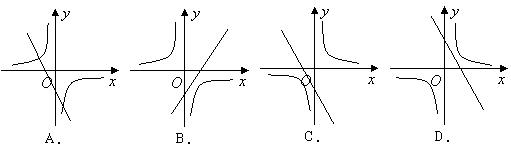
7．函数
与
在同一坐标系中的图象可能是（ ）
8、如图：A、C是函数
的图像上的任意两点，过A作x轴的垂线，垂中足为B，过C作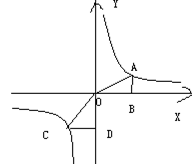
y轴的垂线，垂中足为D，记
的面积为S1，
的面积为S2，则（ ）
A、S1>S2 B、S1=S2 C、S1<S2 D、S1与S2的大小关系不能确定
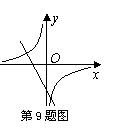9、直线
和双曲线
在直角坐标系中的位置如图所示，下列结论：①k＞0；②b＞0；③k＜0；④b＜0。其中正确的是
A、①② B、②③ C、③④ D、①④
10．下列方程中，没有实数根的方程是（ ）
（A）
； （B）
；
（C）
；
（D）
．
11、已知，二次函数
的图像经过（3，0）和（9，0），则下面的判断中，错误的是（ ）
A、抛物线的对称轴是直线x=6
B、同给出的重要任务不能确定顶点的坐标
C、同给出的条件不能确定抛物线开口向上还是向下
D、抛物线的顶点在第三象限
12、不论k取任何实数，抛物线
的顶点都（
）
A、在直线y=x上 B、y= —x上 C、在x轴上 D、在y轴上
13、若函数
的图象经过第一、三、四象限，则函数
的图象必不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
14、点B与点A(-3,2)关于x轴对称,则点B的坐标为 （ ）
Ａ.(3,-2) Ｂ．(-3,-2) Ｃ.(3,2) Ｄ.(-3,2)
15、根据下表中的规律，从左到右的空格中应依次填写的数字是（ ）
|
|
|
|
|
|
|
|
|
| 000 | 110 | 010 | 111 | 001 | 101 |
A．100，011 B．011，100 C．011，101 D．101，110
二．填空题(本大题共5小题，每小题4分，共20分．把答案填在答题卡相应位置)
16、已知：一次函数
的图象与直线
平行，并且经过点
，那么这个一次函数的解析式是___________________．
17、一家商店计划出售60件衬衫，要使销售总额不低于5100元，则每件衬衫的售价至少应为 元。
18、已知x2＋4x－2=0，那么3x2＋12x＋2000的值为 。
19、若不等式组
的解集是
，则
= ．
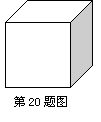
20、下列图形：①等腰三角形；②矩形；③正五边形；④正六边形中，只有三个是可以通过切正方体(如图)面得到的切口平面图形，这三个图形的序号是 。
三．解答题（在答题卷中作答，要有必要的解题步骤．共55分）．
21、（本小题满分5分）解不等式组：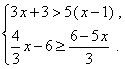
22．（本小题满分5分）现有边长为a的正方形纸片3张，边长为b的正方形纸片1张，长为a,宽为b的长方形纸片4张，请你将它拼成一个长方形，并运用面积之间的关系，将多项式
因式分解。
23、(本题10分）张新和李明相约到图书城去买书,请你根据他们的对话内容(如图),求出李明上次所买书籍的原价.
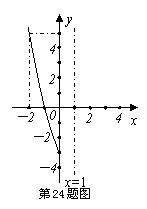
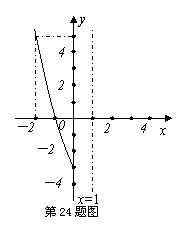
24．（本小题满分10分）已知二次函数
的图象与y轴相交于点(0，－3)，并经过点(－2，5)，它的对称轴是x=1，如图为函数图象的一部分。
（1）求函数解析式，写出函数图象的顶点坐标；(5分)
（2）在原题图上，画出函数图象的其余部分；(2分)
（3）如果点P(n，－2n)在上述抛物线上，求n的值。(3分)
 |
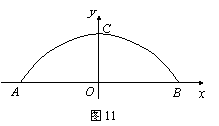
25、（本小题满分12分）一座拱桥的轮廓是抛物线型(如图10所示)，拱高6 m，跨度20 m，相邻两支柱间的距离均为5 m.
(1) 将抛物线放在所给的直角坐标系中(如图11所示)，其表达式是
的形式.
请根据所给的数据求出
的值.
(2) 求支柱MN的长度.
(3) 拱桥下地平面是双向行车道(正中间是一条宽2 m的隔离带)，其中的一条行车道能否
并排行驶宽2 m、高3 m的三辆汽车(汽车间的间隔忽略不计)？请说说你的理由.
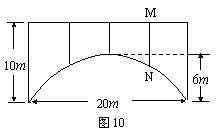
26、（本题12分）
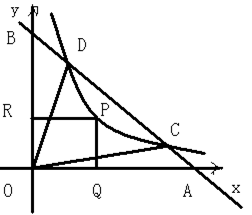
如图，直线AB过点(m,0)，B(0,n) (m>0,n>0)。反比例函数
的图象与AB交于C、D两点。P为双曲线上任一点，过P作PQ⊥x轴于Q，PR⊥y轴于R。
（1）、若m+n=10，n为何值时△AOB面积最大，最大值是多少。
（2）、若
，求n的值。
（3）、在（2）的条件下，过O、D、C三点作抛物线，当该抛物线的对称轴为x=1时，矩形PROQ的面积是多少？
答卷
一．选择题(本大题共15小题，每小题3分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
二．填空题(本大题共5小题，每小题4分，共20分．把答案填在答题卡相应位置)
16、__________ 17、__________ 18、___________19、_________ 20、__________
三．解答题（在答题卷中作答，要有必要的解题步骤．共55分）．
21、（本小题满分5分）
解不等式组：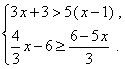
22、（本小题满分5分）
 |
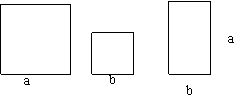23、（本小题满分10分）
 |
24、（本小题满分10分）
25、（本小题满分12分）
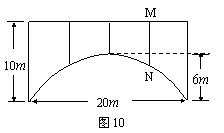
26、（本小题满分12分）
答案
一．选择题(本大题共15小题，每小题3分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A | C | B | C | D | B | A | B | C | B | D | B | A | C | B |
二．填空题(本大题共5小题，每小题4分，共20分．把答案填在答题卡相应位置)
16、
17、85 18、
2006 19、
1
20、①②④
三．解答题（在答题卷中作答，要有必要的解题步骤．共55分）．
21、（本小题满分5分）
解：由① 得
， 解得 
． 由② 得
，解得 
．所以，原不等式组的解集是
22、（本小题满分5分）
|
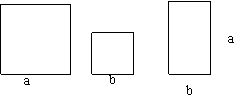23、（本小题满分10分）
解：设李明上次购买书籍的原价是x元,由题意有0.8x+20=x-12,解得x=160.
24、（本小题满分10分）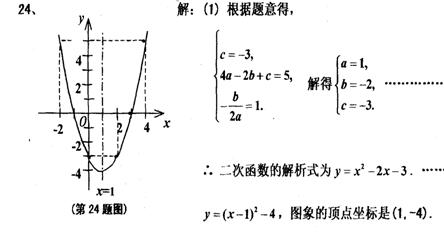
25、（本小题满分12分）
解：(1)根据题目条件，A、B、C的坐标分别是(-10,0)、(0,6)、(10,0). ------------1分
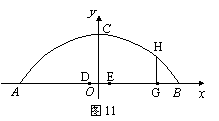将B、C的坐标代入，得
---------------------------------------------3分
解得
. ----------------------------------------------4分
所以抛物线的表达式是
. -------------5分
(2) 可设N(5,
)，于是
. ----------------6分
从而支柱MN的长度是
米. ---------------------------7分
(3) 设DE是隔离带的宽，EG是三辆车的宽度和，则G点坐标是(7,0)(7＝2÷2＋2×3).
-8分
过G点作GH垂直AB交抛物线于H，则
. ---------9分
根据抛物线的特点，可知一条行车道能并排行驶这样的三辆汽车. ----------------------------10分
26、（本小题满分12分）
解：当n=5时，
取最大值
（2）、
提示：当时，则有AC=CD=DB，过C、D作垂线，则C、D的横坐标为，
。
(3)、