面积问题与面积方法
姓名：
例1 已知△ABC中三边长分别为a，b，c，对应边上的高分别为ha=4，hb=5，hc=3．求a∶b∶c．
例2
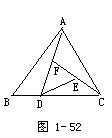
如图1－51，
ABCD的面积为64平方厘米(cm2)，E，F分别为AB，AD的中点，求△CEF的面积．
例4 用面积方法证明：三角形两边中点连线平行于第三边．
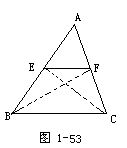
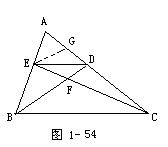
例5 如图1－54．在△ABC中，E是AB的中点，D是AC上的一点，且AD∶DC=2∶3，BD与CE交于F， S△ABC=40，求SAEFD．
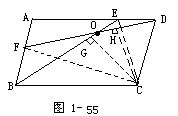
例6 如图1-55所示．E，F分别是
ABCD的边AD，AB上的点，且BE=DF，BE与DF交于O．求证：C点到BE的距离等于它到DF的距离．
练习：
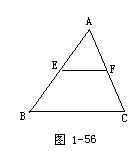
1．如图1－56所示．在△ABC中，EF∥BC，且AE∶EB=m，求证：AF∶FC=m．
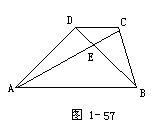
2．如图 1－57所示．在梯形 ABCD中， AB∥CD．若△DCE的面积是△DCB的面积的四分之一，问：△DCE的面积是△ABD的面积的几分之几？
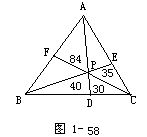
3．如图1－58所示．已知P为△ABC内一点，AP，BP，CP分别与对边交于D，E，F，把△ABC分成六个小三角形，其中四个小三角形的面积已在图中给出．求△ABC的面积．
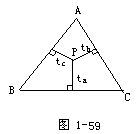
4．如图1－59所示．P为△ABC内任意一点，三边a，b，c的高分别为ha，hb，hc，且P到a，b，c的距离分别为ta，tb，tc．
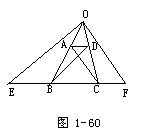5．如图1－60所示．在梯形ABCD中，两腰BA，CD的延长线相交于O，OE∥DB，OF∥AC且分别交直线BC于E，F．求证：BE=CF．
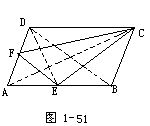
6．如图1－61所示．P是△ABC的AC边的中点，PQ⊥AC交AB延长线于Q，BR⊥AC于R．
求证：
