上虞市2006年初中毕业生学业考试适应性练习
数 学
第 Ⅱ 卷 （非选择题 共110分）
注意事项：
1．第Ⅱ卷3至8页，用钢笔或圆珠笔直接答在试卷上．
2．答题前，将密封线内的项目写清楚．
| 题 次 | 二 （11—16） | 三 | 总 分 | |||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |||
| 得 分 | ||||||||||
| 阅卷人 | ||||||||||
二、填空题（本题有6小题，每小题5分，共30分）
11．勤俭节约是中国人民的传统美德．如果节约5元记作＋5元，那么浪费2元
记作 元．
12．据中国统计信息网公布，截止2005年11月1日零时，全国31个省、自治区、直辖
市和现役军人的人口总数约为人．用科学记数法表示这个数是 ．
13．若实数m,n满足条件m+n=3，且m-n=1，则m=______，n=______．
14．有6张背面相同的扑克牌，正面上的数字分别是3，4，5，6，7，8．若将这六张牌背面朝上洗匀后，从中任意抽取一张，那么这张牌正面上的数字是偶数的概率为______．
15．如图，已知正方形ABCD的边长为2.如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′点处，那么cot∠D′等于________．
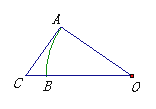16．如图，OAB是以6cm为半径的扇形，AC切弧AB于点A交OB的延长线于点C,如果弧AB的长等于3cm,AC=4cm,则图中阴影部分的面积为_________．
三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17.（1）计算：
.
（2）解方程：
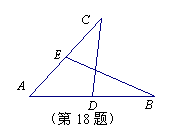18.已知：如图，AB＝AC,AE＝AD，点D、E分别在AB、AC上．
求证：∠B＝∠C．
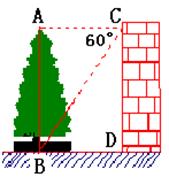19．如图，小聪想估测家门前的一棵树的高度，他站在窗户C处，观察到树顶端A正好与C处在同一水平线上，小聪测得树底B的俯角为60°，并发现B点距墙脚D之间恰好铺设有六块边长为0.5米的正方形地砖，因此测算出B点到墙脚之间的距离为3米，请你帮助小聪算出树的高度AB约多少米？（结果保留1位小数；参考数据：
，
）
20．如图，有一块三角形土地，它的一边BC=100米，高AH=80米，某单位要沿着一边BC修一座底面是矩形DEFG的大楼，D、G分别在边AB、AC上．
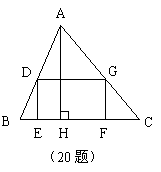若大楼的宽DE是长EF的
，求这个矩形的面积．
21．已知平行四边形ABCD有三个顶点在坐标轴上，A、B两点的坐标分别为（－2，0）、（0，3），且AD＝4．请你在备用的坐标系中画出两个符合条件的平行四边形，并写出此时C、D两点的坐标．
 |  | ||
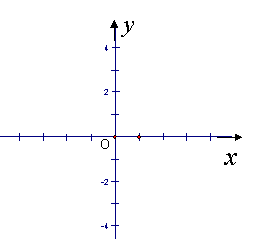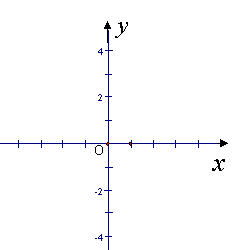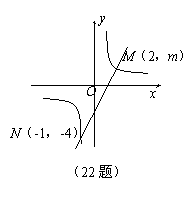
22.如图，一次函数
的图象与反比例函数
的图象交于M、N两点.
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
23.水产经营户王大伯原计划以7.2元/千克的价格出售400条鳙鱼（俗称胖头鱼），现为了满足顾客需要,决定将所有鳙鱼分成鱼头和鱼身(也称鱼尾巴)两段出售,按市场行情, 鱼头价格为鱼身价格的1.5倍.以下是王大伯随机抽取的5条鳙鱼分成两段前后的质量情况：
| 顺序号 | 1 | 2 | 3 | 4 | 5 | |
| 分成两段前的质量（单位：千克） | 2.1 | 1.9 | 2.2 | 1.8 | 2 | |
| 分成两段后的质量 （单位：千克） | 鱼头 | 0.8 | 0.7 | 0.8 | 0.6 | 0.7 |
| 鱼身 | 1.1 | 1.0 | 1.2 | 1.0 | 1.1 | |
（1）从400条鳙鱼中随机抽取的5条，分成两段前的平均质量是 千克，以此估算这400条鳙鱼分成两段前的总质量是 千克；抽取的5条鳙鱼分成两段后的平均质量是 千克，鱼头与鱼身的质量比为 ；
（2）根据（1）的结果，要使分成两段后的400条鳙鱼的销售总额与按原计划的销售总额相同，那么分成两段后鳙鱼的平均价格是多少？
（3）在（2）中，王大伯应以怎样的价格出售鱼身和鱼头？（精确到0.1元）
24．如图，已知△ABC的三个顶点都在格点上，且点A在Y轴上．
（1）将△ABC绕A点按逆时针旋转90°，请作出旋转后的△
；
（2）若抛物线
经过（1）中的
、
两点，且该抛物线的顶点P与、所组成的△
∽△CBA，求此抛物线的解析式；
（3）若将△ABC沿第一、第三象限的角平分线翻折，得△
，问△斜边的中点是否在（2）中所求抛物线的对称轴上，请说明你判断的理由．
上虞市2006年初中毕业生学业考试适应性练习
数学参考解答及评分意见
一、选择题（本题10小题，每小题4分，共40分）：D D A B D C B A C D
二、填空题（本题6小题，每小题5分，共30分）
11．-2 12．
13．2，1 14．
15．
16．3
，其中单位1分
三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17．（１）解：原式=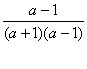
+
……（１分）
=
+ （2分） =
.…（3分）= 1 …（4分） (省略1-2个步骤不扣分)
（2）移项，分解因式正确得2分，答案正确得2分（少一个扣1分）共4分
18．证明：在△ABE和△ACD中，
∵∠BAE＝∠CAD (或∠A＝∠A) ……（3分）
又∵ AB＝AC, AE＝AD,
∴ △ABE≌△ACD . .…（6分） ∴∠B＝∠C . …（8分）
19．写出AC=BD=3米（2分），在Rt△ABC中，tan60°=
（4分），
AB=AC×tan60°（5分）=3
（6分）≈3×1.732≈5.2 (米) （8分）
20. 写出△ADG∽△ABC及比例式（3分）求出矩形的长50米和宽40米（6分），得到矩形的面积为2000平方米（8分）
21．符合条件的平行四边形较多，以下四个解供参考：
解一：如图1，C、D的坐标分别为（－4，3）、（－6，0）．
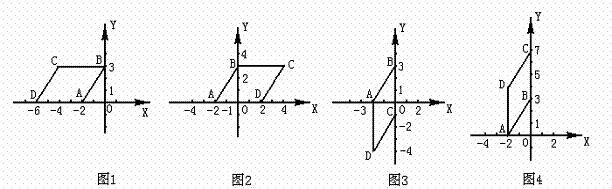解二：如图2，C、D的坐标分别为（4，3）、（2，0）．
解三：如图3，C、D的坐标分别为（0，－1）、（－2，－4）．
解四：如图4，C、D的坐标分别为（0，7）、（－2，4）．
评分意见：画图正确一个得2分；坐标写对得3分，共5×2=10分．
22.（1）将N（
1，4）代入中 得k=4……（2分）
所以，反比例函数的解析式为
………（3分）
将M（2，m）代入解析式中 得m=2………（4分）
将M（2，2），N（1，4）代入中
解得a=2 b=-2……（7分）
所以，一次函数的解析式为
……（8分）
（2）由图象可知：当1＜x＜0或x＞2时一次函数的值大于反比例函数的值.（12分）
23．（1）2 800 1.8 2:3 （4分）
(2)设分成两段后鳙鱼的平均价格是
元，由题意得：
（6分）
解得=8元，即分成两段后鳙鱼的平均价格是8元/千克（8分）．
（3）鱼身的价格约为6.7元/千克，鱼头的价格为10元/千克（12分）．
24．解：（1）如图△A1B1C1就是所求（3分）
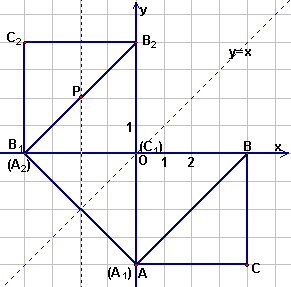（2）由(1)可知，B1（－4，0），C1（0，0）， （4分）
∵△P B1C1∽△CBA,
∴∠B1PC1=Rt∠．（5分）
由此得P(－2，2)或P(－2，－2)．（7分）
当P(－2，2) 时，
可得抛物线的解析式为
．（9分）
当P(－2，－2) 时，可得解析式为
．（11分）
（3）所得三角形斜边上的中点在两个抛物线的对称轴上．（12分）
理由是：如图，将△ABC沿第一、三象限的角平分线（y=x）翻折，得△A２B２C２，知斜边A２B２的中点为（－2，2），（13分）而已求两抛物线的对称轴都为直线x=－2，所以，△A２B２C２斜边上中点在抛物线的对称轴上．（14分）