第二章〈〈方程〉〉 检测
一．选择题（每小题5分，共30分）
1．下列方程中，两个根的和是2的一元二次方程是（ ）
A．
B．
C．
D．
2．设
，则方程
就变形为（
）
A．
B．
C．
D．
3．新兴电视机厂由于改进技术，降低成本，电视机售价连续两次降价10%，降价后每抬售价为
元，该厂的电视机每台原价应为（ ）
A．
元
B．
元 C．
元
D．
元
4．（2003青岛）已知
，
，且
，则
的值为（
）
A．2 B．-2 C．-1 D．0
5．若关于
的二次方程
中，
，且
，则方程的两根（ ）
A．相等 B．同为正 C．一正一负 D．同为负
6．下列命题中，错误的是（ ）
A． 对于一元二次方程
，若
，则一定有一个根是1；若有一个根是1，则一定有；
B． 对于一元二次方程，若
，则一定有一个根是-1；若有一个根是-1，则一定有；
C． 若
是方程的两个根，则
；
D．在实数范围内，二次三项式
总可以分解为两个一次因式的积.
二．填空题（每小题5分，共20分）
7．若一元二次方程
有实数根，则的取值范围是
.
8．方程
的实数根的个数有
个.
9．（2003杭州）浙江万马篮球队某主力队员，在一次比赛中22投14中得28分，除了3个三分球外，他还投中了 个两分球和 个罚球.
10．已知方程
的两根的平方和比它们的积大21，则
=
.
三．简答题（共50分）
11．解下列方程或方程组：
（1）（6分）
；
（2）（6分）（2003宁波）
=4；
（3）（6分）
；
（4）（6分）（2004北京）
；
（5）（6分）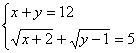
.
12．（8分）已知方程
=0一个根为
，求另一个根及的值.
13．（12分）设是关于的方程
的两个实数根，
（1） 求
取何值时，
有最小值？最小值为多少？
（2） （2）当=11时，求作一个关于的方程，使它的一个根使
，另一个根是
.
四．探索题（共20分）
14．（8分）设实数
满足
，则
=
.
解题过程：
15．已知
分别为△ABC中∠A，∠B，∠C的对边，并且方程
有实数根，若△ABC中，∠A=∠C，方程有两个不相等的实数根，且满足
=1，求∠B的度数.