白洋中学九上数学九月考试卷
班级 考号 姓名 分数
一、选择题（每题3分，共30分）
1、等腰三角形中，有一个角为45°，那么这个三角形是（ ）
A、锐角三角形 B、直角三角形 Ｃ、钝角三角形 Ｄ、锐角三角形或直角三角形
2、使两个直角三角形全等的条件是（ ）
A、两直角边对应相等 B、一锐角对应相等 C、两锐角对应相等 D、斜边相等
3、已知某三角形的周长是6，顺次连接该三角形三边中点所成三角形的周长是（ ）
A、 2 B、3 C、1.5 D、12
4、下列命题中，逆命题正确的（ ）
A、对顶角相等 B、直角相等
C、同旁内角互补，两直线平行 D、等边三角形是等腰三角形
5、化简
的结果是（ ）
A、2
B、5
C、2
D、4
6、到三角形的三边距离相等的点是（ ）
A、三条高的交点 B、三条中线的交点 C、三条角平分线的交点 D、三条边的中垂线交点
7、关于四边形ABCD ，①两组对角分别相等；②两组对边分别相等；③一组对边平行且相等；④对角线AC和BD相等；以上四项条件中可以判定四边形ABCD是平行四边形的有（ ）
A、1个 B、 2个 C、 3个 D、4个
8、能把一个三角形分成面积相等的两部分的是三角形的（ ）
A、中线 B、高线 C、角平分线 D、任一边的垂直平分线
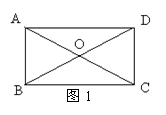
9、如图1：矩形ABCD的对角线AC、BD相交于O，如果△ABC
的周长比△AOB的周长大10cm，则矩形边BC的长是（ ）
A、5cm B、10cm C、7.5cm D、不能确定
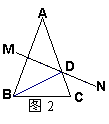
10、如图2，AB=AC，∠A=40°，AB的垂直平分线MN交AC于D，
则∠DBC=（ ）
A、30° B、20° C、15° D、10°
二、填空题（每题3分，共15分）
11、Rt△ABC 中，∠C=90O，CD是斜边AB的中线，
若CD=3cm，则AB= ㎝。
12、当
时，
无意义。
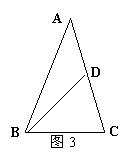
13、已知，如图3,△ABC中AB=AC，点D在AC上，且BD=BC=AD，
则∠A的度数为 。
14、若点（0，2）在直线y=3x＋b，则b= .
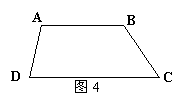
15、如图4，在梯形ABCD中，AB∥CD,∠D=80°，∠C=50°，
若AB=4㎝，CD=7㎝，则腰AD的长为 ㎝。
三、解答题（每题6分，共24分）
16、计算：（－
）0＋（－3）2×（－2）3
17、解方程：（x－1）＋1＝2（x－1）
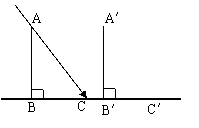
18、如图，太阳光线AC与A′C′是平行的，同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗？说说你的理由。
19、如图，在等腰梯形ABCD中，AD∥BC,AB＝DC
⑴利用尺规作底边作底边AD的中点E。（保留作图痕迹，
不写作法和证明）
⑵连接EB，EC求证：∠ABE＝∠DCE
四、解答题（每题7分，共21分）
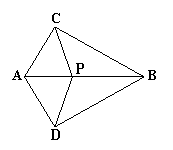
20、已知：∠ACB=∠ADB=900，AC=AD，P是AB上任意一点，
求证：CP=DP
21、某商店出售两件衣服，售价均为60元，其中一件赚25%，而另一件亏25%，那么这
家商店是赚了还是亏了，或是不赚也不亏呢？请通过计算说明理由。
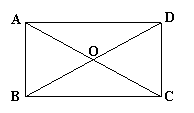
22、如图，在矩形ABCD中，两条对角线AC、BD相交于点O，AB=4cm ,AD=
cm，
试判定△AOB的形状，并说明理由。
 |
五、解答题（每题10分，共30分）
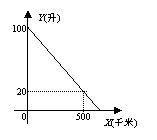23、某汽车生产厂对其生产的A型汽车进行耗油量实验，实验中汽车视为匀速行驶。已知油箱中的余油量y（升）与行驶时间t（小时）的关系如下表，与行驶
路程x（千米）的关系如下图。请你根据这些信息求A型车在实
验中的速度。
| 行驶时间t（小时） | 0 | 1 | 2 | 3 |
| 余油量y（升） | 100 | 84 | 68 | 52 |
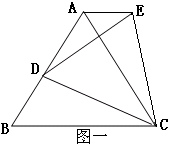
24、⑴如图一，等边三角形ABC中，D是AB边上的动点，以CD为一边，向上作等边△EDC，连接AE，求证：AE∥BC
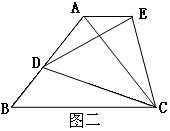
⑵如图二，将⑴中等边三角形改成以BC为底边的等腰三角形，所作△EDC改成相似于
△ABC，请问：是否仍有AE∥BC？证明你的结论。
25、我国人均年用纸量约为28公斤，每个初中毕业生离校时大约有10公斤废纸。用1吨废纸造出的再生好纸，所能节约的造纸木材相当于18棵大树，而平均每亩森林只有50至80棵这样的大树。
⑴若某地区2006年5万初中毕业生环保意识较强，他们能把自己离校时的全部废纸送到回收站使之制造为再生好纸，那么最少可使多少亩森林免遭砍伐？
⑵某地区从2005年初开始实施天然林保护工程，到2006年初成效显著，森林面积大约由110万亩增加到121万亩。假设该地区年用纸量的15%可以作为废纸回收利用，并且森林面积年增长率保持不变，请你按该地区总人数为400万人计算：在从2006年初到2007年初这一年度内，该地区新增加的森林面积与因废纸回收利用所能保护的森林面积之和最多能达到多少亩？