福建省数学奥林匹克学校
2004年暑期培训新初三数学竞赛试卷
第一试
(考试日期：2004年7月26日上午8∶00 考试时间120分钟 满分100分)
(考生注意：请将所有答案填写在答卷纸上，否则不计分)
一、 选择题(每小题4分，共40分)
1、若
，则
、
、
这三个数的大小顺序是 （ ）
A、
B、
C、
D、
2、下列各值中最大的是 （ ）
A、
B、
C、
D、
3、若
、
、
都是有理数，则
、
的值是 （ ）
A、二者均为有理数 B、二者均为无理数
C、一个为无理数，另一个为有理数 D、以上三种情况均在可能
4、分子为1，分母为大于1的自然数的分数叫做单位分数。若将
表示分母不同的两个单位分数之和，则所有可能的表示组数有 （ ）
A、1组 B、2组 C、3组 D、4组
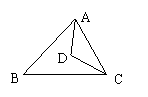5、如图，已知
中，AB＝AC，
和
的平分线相交于D点，
，那么
的大小是 （ ）
A、
B、
C、
D、
6、已知的三边分别为
：（1）以
为三边的三角形一定存在；（2）以
为三边的三角形一定存在；（3）以
为三边的三角形一定存在；（4）以
为三边的三角形一定存在。以上四个结论中，正确结论的个数为（）
A、1 B、2 C、3 D、4
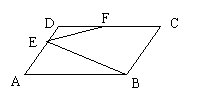
7、如图，在
中，AB＝2BC，BE
AD于E，F为CD中点，设
，
，则下面结论成立的是 （ ）
A、
B、
C、
D、
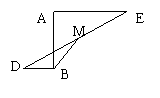
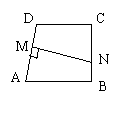8、如图，在梯形ABCD中，AB//CD，
，AB＝9厘米，BC＝8厘米，CD＝7厘米，M是AD的中点，从M作AD的垂线交BC于N，则BN的长等于（ ）
A、1厘米 B、1.5厘米 C、2厘米 D、2.5厘米
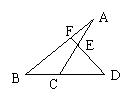
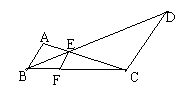
9、如图，D是的BC边延长线上一点，且CD＝BC，E是AC的中点，DE的延长线交AB于F，则DE:EF等于 （ ）
A、2 B、3 C、
D、
10、已知：在ΔABC中，∠ACB=90º，∠ABC=15º，AC=1，则BC的长为（ ）
（A）2+
（B）
（C）0.3 （D）
二、 填空题(每小题4分，共40分)
11、已知
，
，那么
。
12、已知A＝
，化简后，A＝ 。
13、已知
与
是同类根式，则
的值为 。
14、由下列等式
，
，
，…所揭示的规律，可得出一般的结论是 。
15、已知在中，
，且
，则
的取值范围是 。
16、如图，已知AB＝4，DBAB，EAAB，DB＝3，EA＝6，又点M是DE的中点，则BM的长等于 。
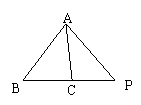
17、如图，在中，AB=8，BC=7，CA＝6，延长BC至P，使得
，则PC等于 。
18、从等边三角形内一点向三边作垂线，已知这三条垂线长分别为1、3、5，则这个等边三角形的面积是
19、A、B、C、D、E、F六个足球队进行单循环赛，当比赛进行到某一天时，统计出A、B、C、D、E五队已分别比赛了5，4，3，2，1场球，由此可知，还没有与B队比赛的球队是 。
20、如图，AB∥EF∥CD，已知AB=10，CD=40，则EF= .
三、解答题（每小题10分，共计20分）
21、如图，设P是等边的BC边上任一点，连结AP，作AP的中垂线交AB、AC于M、N。
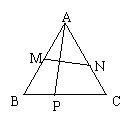证明：BP
PC＝BMCN
22、已知：如图，边长为a的菱形ABCD中，∠DAB=60º，E是异于A、D两点的动点，F是CD上的动点，满足：AE+CF=a.
求证：无论E、F怎样移动，
BEF总是正三角形.
参考答案
一、选择题（每小题4分，共计40分）：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | A | C | D | C | B | A | B | A |
二、填空题：（每小题4分，共计40分）
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
| 8 |
（n为大于等于1的自然数） |
|
| 题号 | 16 | 17 | 18 | 19 | 20 |
| 答案 | 2.5 | 9 |
| E队 | 8 |
三、解答题（每小题10分，共计20分）
21、如图，设P是等边的BC边上任一点，连结AP，作AP的中垂线交AB、AC于M、N。
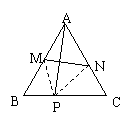证明：BPPC＝BMCN
证明：连接PM、PN。
MN是AP的中垂线，则
，
有
。
可推得：
，
，故BPPC＝BMCN
22、已知：如图，边长为a的菱形ABCD中，∠DAB=60º，E是异于A、D两点的动点，F是CD上的动点，满足：AE+CF=a.
求证：无论E、F怎样移动，BEF总是正三角形.
证明：连结DB
可证得
则EB=FB，
又
，
，
即BEF为正三角形。