2004—2005学年度第一学期期末考试
初三数学科模拟试题
说明：本卷满分120分，考试时间90分钟
一、选择题（每小题3分，共15分）
1、在△ABC中，∠C=90°，BC=2，AB=3，则下列结论正确的是（ ）.
A．sinA=
B．cosA=
C．sinA=
D．tanA=
2、函数y=(2m－1)x是正比例函数，且y随自变量x的增大而增大，则m的取值范围是
A、m<
B、m>
C、m≥ D、m≤
3、已知3是关于x的方程
的一个解，则2a的值是（ ）
A、11 B、12 C、13 D、14
4、有命题：①相等的圆心角所对的弧相等；②相等的弦所对的弧相等；③直径所对的圆周角是直角；④垂直于弦的直径平分这条弦；⑤经过圆心的每一条直线都是该圆的对称轴. 其中真命题的个数为( )
A、1个 B、2个 C、3个 D、4个
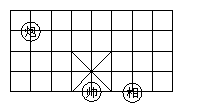
5、如图所示的象棋盘上，若帅位于点（1，－2）上，相位于点（3，－2）上，则炮位于( )
A. （－1，1） B. （－1，2）
C. （－2，1） D. （－2，2）
二、填空题（每小题4分，共20分）
6、在函数
中，自变量x的取值范围是
．
7、若 sinA – + ( cotB – )2 = 0，则△ABC是___________三角形．
8、已知一元二次方程
，当
时方程有两个相等
的实数根．
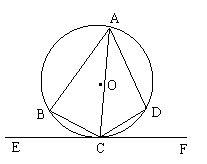9、圆内接四边形ABCD中，AC平分
∠BAD，EF切圆于C，若∠BCD=120º，
则∠BCE= ．
10、一个直角三角形的斜边为13cm，面积为30 cm2，则它的内切圆的半径
为 cm．
三、解答下列各题（每小题6分，共30分）
11、计算：
12、解方程组：
13、用换元法解方程
14、尺规作图：（保留作图痕迹，不要求写作法和证明）
有一只老鼠藏身在地面上的A，B，C的任一个洞里(如图所示)，
请你为猫设计一个最佳的位置抓老鼠．
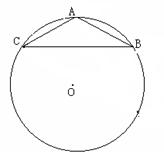
15、如图，已知△ABC外接于⊙O，AB＝AC＝5cm，∠A=120o，求⊙O的直径．
四、（每小题7分，共28分）
16、已知平面直角坐标系中A、B、C三个点，点A的坐标为（1，2），
点B和点A关于原点对称，点C为直线y＝2x＋3与y轴的交点．
（1）求点B、C的坐标；
（2）试判断点D（－2，5）是否落在直线BC上？
17、某服装厂在销售中发现某种衬衫平均每天可售出20件，每件盈利40元。
为了迎接元旦节，该服装厂决定采取适当的降价措施，扩大销售量，增加
盈利，减少库存，经市场调查发现：如果每件衬衫每降价1元，那么平均
每天就可多售出2件。设每件衬衫降价x元。
（1）试求出衬衫售出件数y与x之间的函数关系式，并指出y是x的什么
函数；
（2）要想平均每天在销售这种衬衫上盈利1200元，求出满足题意的x值。
18、以下是小明同学填写实习报告的部分内容：
题目：在两岸近似平行的河段上测量河宽；
测得数据：∠CAD＝60°，AB＝20米，∠CBD＝45°，∠BDC＝90°；
测量目标图示：请你根据以上的条件，计算出河宽CD（结果保留根号）．
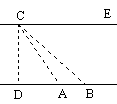
19、已知x1、x2是关于x的方程x2－6x＋k=0的两个实数根，且满足
x12x22－x1－x2=115．
（1）求k的值； （2）求x12+x22+8的值．
五、（每小题9分，共27分）
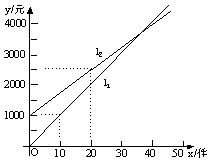
20、如图，
反映了某个体服装老板的销售收入与销售量之间的关系，
反映了该老板的销售成本与销售量的关系图，根据图象填空：
（1）当销售量为60件时，销售收入为
元，销售成本为 元．
（2）当销售量为30件时，销售收入为 元，销售成本为 元．
（3）对应的函数的表达式是：
．
对应的函数的表达式是：
．
（4）当销售量为 件时，销售收入等于销售成本
（5）当销售量为 件时，该老板赢利，当销售量为 件时，
该老板亏本．
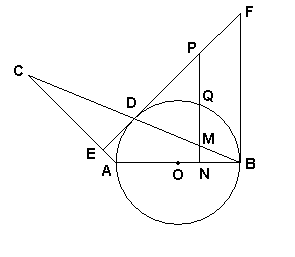
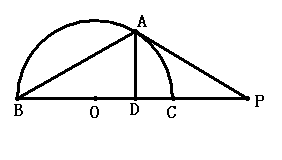
21、如图，BC是半圆的直径，O是圆心，P是BC延长线上一点，PA切半圆
于点A，AD⊥BC于点D.
(1) 若∠B=30°，问：AB与AP是否相等？请说明理由；
(2) 求证：PD·PO=PC·PB；
(3) 若BD：DC=4：1，且BC=10，求PC的长.
22、如图，AD是⊙O的直径，⊙O过CB的中点D，直线FE过点D，且
FE⊥AC于E，FB切⊙O于B，P是线段DF上一动点，过P作PN⊥AB于N，PN与⊙O交于点Q，与DB交于点M.
（1）求证：FE是⊙O的切线；
（2）若∠ABD＝30°，AB＝2，设DP＝x，MN＝y，求y与x之间的函数关系式，并指出自变量x的取值范围；
（3）在（2）中，当x为何值时，PQ∶PN＝1∶5？
