与函数有关的中考题（奥校讲义）
1． 已知二次函数
的图象与x轴交于A、B，C是线段AB的中点，M是抛物线上位于x轴上方的动点，且∠AMB为锐角，求MC的取值范围。
2． 已知抛物线
不经过第三象限。（1）求
和
的取值范围；（2）若抛物线与x轴有交点
，且顶点在正比例函数
的图象上。求此抛物线的解析式。
3． 一次函数
的图象和某二次函数图象的两个交点A、B恰好在坐标轴上，对称轴是直线
，已知B
，AB
，求这两个函数的解析式。
4． 
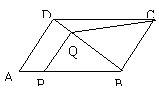
如图，在 ABCD中，AB=5，AD=3，sinA=
，P为AB上一个动点（P不与A、B重合），过P作PQ∥AD交BD于Q，设AP的长为x，
四边形QPBC的面积为y，求y与x的函数关系式及自
变量x的取值范围。
5． 为何值时，反比例函数
的图象与一次函数
的图象只有一个交点。
6． 已知反比例函数
的图象与一次函数
的图象都经过P
。（1）求这个一次函数的解析式；（2）如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上，顶点C、D在这个反比例函数的图象上，两底AD、BC与y轴平行，且A、B的横坐标分别为和
，求的值。
7． 已知抛物线
。（1）求证：无论
为什么实数，抛物线恒经过x轴上一定点；（2）设抛物线与y轴交于C点，与x轴交于A
、B
两点，且满足
。问：过A、B、C三点的圆与抛物线是否有第四个交点？试说明理由，如果有，求出其坐标。
8． 
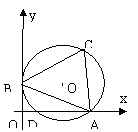如图：已知一次函数
的图象与x轴、y轴分别交
于A、B两点，以AB为边在第一象限作一正三角形ABC，⊙O，
为ΔABC的外接圆，与x轴交于点D。（1）求C点的坐标；求过
D、O，、A三点的二次函数的解析式，并求该函数的最值。
 |
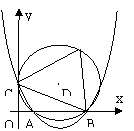9． 如图：抛物线
交x轴正方向于A、B两点，
交y轴正方向于C点。过A、B、C三点作⊙D，若⊙D与y轴相
切。（1）求
满足的关系式；（2）设∠ACB=α，求tanα；
（3）设抛物线顶点为P，判断直线PA与⊙D的位置关系，并证明。
 |
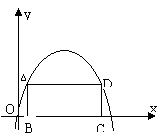10． 如图：矩形ABCD的顶点B、C在x轴的正半轴上，A、D
在抛物线
上，矩形的顶点均为动点，且矩形在
抛物线与x轴围成的区域里。（1）设点A的坐标为
，试
求矩形的周长p关于变量x的函数的解析式，并写出x的取值范围；
（2）是否存在这样的矩形ABCD，它的周长p=9？试证明你的结论。
11．
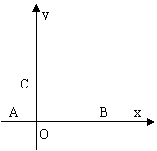
如图：已知抛物线
，x轴
交于A、B两点（点A在点B的左边），与y轴交于点C。
（！）写出A、B、C各点的坐标（可用含
的式子表示）；
（2）若ΔABC的面积为15，求此抛物线的解析式。
（3）过点E
作ED∥AC，在第一象限交抛物线于点D，
求ED的函数的解析式，问四边形AEDC的形状并求其面积，
证明你的结论。
12．
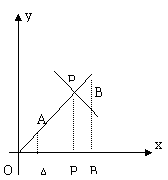12．如图：已知抛物线
和直线
，它们的一个交点的纵坐标为4。（1）求此抛物线和直线的解析式。
（2）如果直线
与（1）中的抛物线交于
A、B两个不同的点，和（1）中的直线交于点P，分别
过A、B、P作x轴的垂线，垂足为A，、B，、P，，证明：
；（3）在（2）中能否选取适当的
的值，使得
，如果能，求此时的值；
如果不能，请说明理由。
13.已知是大于2的整数，设抛物线
与x轴有两个交点，与y轴交于A点；直线
经过抛物线的顶点M，并与抛物线交于B点（此时
），与y轴交于C点。
（1） 求
和
的解析式；（2）求证：y轴与ABM的外接圆切于A；
（2） 若ΔABM的外接圆是⊙N，过C作⊙N的切线（切点为T）交x轴于S，连接NS，求证NS2 = ST·SC。
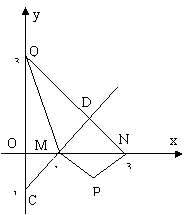14．如图：抛物线
的顶点为P，
与x轴交于M、N两点（M在N的左边），ΔPMN
的三个内角∠P、∠M、∠N所对的边是
且
若关于
的方程
有两个相等的实根。
（！）试判定ΔPMN的形状；
（2）当顶点P的坐标为（2，-1），求抛物线的解析式。
（3） 设抛物线与y轴交于Q点，求证：直线
将四边形MPNQ分成的两个图形的面积相等。
15．已知：
是ΔABC的∠A、∠B、∠C的对边，抛物线
交x轴于两点M、N，y轴交于点P，其中点M的坐标是
。
（1） 求证：ΔABC是直角三角形；
（2） 若ΔMNP的面积是ΔNOP的面积的3倍，①求cosC的值；②试判断ΔABC的三边长能否取一组适当的值，使以MN为直径的圆心恰好是抛物线的顶点？如能，求出这组值；如不能，说明理由。
| |
16．已知在x轴的正半轴上有A点，在y轴的正半轴上有B、C两点，且B在C的下方，BC
的长为2，把过A、B、C三点的圆记为⊙Q，∠BAC =∠α。
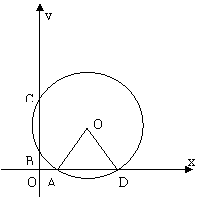（1）试判断x轴与⊙Q的位置关系；若在x轴的的正半轴上有P点，且P与A不重合，再判断∠α与∠BPC的大小（不需证明）；
（2）若B点的坐标为（0，1）指出当x轴与⊙Q为何关系时，
∠α最大？求出当∠α最大时，A点的坐标；
（3） 如图，，若⊙Q与x轴交于A、D两点，弦AD分⊙Q
所成的劣弧与优弧的长度之比为1∶3，且Q点在直线
上，求过Q、A、D三点的抛物线的解析式；
（4） 在（3）中的抛物线上是否存在点E，
使SΔEAD∶SΔAQC = 15∶4？若存在，求出E点的坐标；
若不存在，请说明理由。
17．若关于x的一元二次方程
有两个实数根，又知分别是ΔABC的∠A、∠B、∠C的对边，∠C=90。，且cosB = 
。是否存在整数，使上述的一元二次方程两个实数根的平方和等于RtΔABC的斜边c的平方？若存在，请求出满足条件的m的值；若不存在，请说明理由。
| | ||||
| | ||||