数学试卷
(时间100分钟，满分100分)
一. 填空:（每小题2分，共30分）
1.
=____________.
2.比较2100与375的大小________________.
3.已知y1=x2-7x+6,y2=7x-3,且y=y1+xy2,当x=2时,y=________.
4.如图(1)已知AB∥DE,则∠B+∠C+∠D=___________.
5.一个角比它的补角的一半还小18º24’36’’,则这个角是_________.
6.(1)小明今天买了5本书;(2)2002年美国在阿富汗的战争每月耗费10亿美元;(3)有关部门预测:2002年以DVD形式出售的影片将首次超过盒式录象带,达到95亿美元;(4)人的大脑有个细胞.(5)这次测验小红得了92分.(6)地球上煤储量为15万亿吨以上.上述数据中,精确的有_________,近似的有_____________(填序号).
7.如果4x2-axy+9y2是一个完全平方式,则a的值是________.
8.已知1+x+x2+x3=0,则x+x2+x3+……+x2004的值是_________.
9.a,b,c是ΔABC的三边,且满足a2+b2=25,a2-b2=7,c=5,
则ΔABC最大边上的高是_________.
10.如图(2)矩形ABCD中,DE⊥AC于E,设∠ADE=
,
且
,AB=4,则AD=_______.
11.如图(3)有一个圆柱形的油桶,它的高是80,底面直径是50.
在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点
在同侧的B点处的食物,但由于A,B两点间有障碍,不能直接
到达,蚂蚁只能沿桶壁爬行,则蚂蚁需要爬行的最短路程是_________(
取整数3).
12.如果方程x2+px+1=0(p>0)的两根之差是1,则p=________.
13.若a为整数,且点M(3a-9,2a-10)在第四象限,则a2+1的值是_______.
14.如图(4)在正方形ABCD中,点E在AB边上,且AE∶EB=2∶1,
AF⊥DE于G,交BC于F,则ΔAEG的面积与四边形BEGF
的面积比是_________.
15.已知圆内接四边形ABCD中,对角线AC⊥BD,AB>CD,若CD=4,
则AB的弦心距是____.
二. 选择:(每小题3分,共15分)
( )1.一辆汽车在广场上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是
A.第一次向右拐50º,第二次向左拐130º; B.第一次向左拐30º,第二次向右拐30º;
C.第一次向右拐60º,第二次向右拐120º; D.第一次向左拐40º,第二次向左拐40º.
( )2.在M1=2.02
10-6, M2=0., M3=0.,
M4=6.0610-5四个数中,存在两个数,其中一个数是另一个数的3倍,这两个数为
A.M2与M4,且M4=3M2;
B.M1与M3,且M3=3M1;
C.M1与M4,且M4=3M1; D.M2与M3,且M3=3M2.
( )3.无论m为何值时,二次函数y=x2+(2-m)x+m的图象总过的点是
A (1,3) B (1,0) C (-1,3) D (-1,0).
( )4.关于x的方程(m-2)x2-2x+1=0有实根,则m的取值范围是
A.m<3; B.m
3;
C.m<3且m
2;
D.m3且m2.
( )5.如图(5)在RtΔABC中,∠C=90º,AC=4,BC=3,以BC上一点O为圆心作⊙O与AC,AB相切,又⊙O与BC的另一交点为D,则线段BD的长为
A. 1; B. 
; C. 
; D. 
.
三. 解答:(每小题4分,共20分)
1.已知
,求
的值.
2.某市为了改变市容市貌,提高人民的生活水平,市政府投入巨额资金拆掉大批小平房,建成风景秀丽的无业小区,如图(6)所示是四个物业小区,分别用A,B,C,D表示.为了使四个小区中的孩子能就近上学,市政府准备修建一所小学H,问H应建在何处,才能使四个小区的孩子上学走路的总和最小,请你找出H的位置,并说明理由.
3.如图(7)A市气象站测得台风中心在A市的正东方向300千米的B处,以
千米/时的速度向北偏西60º的BF方向移动.距台风中心200千米范围内是受台风影响的区域.
(1) A市是否会受到这次台风的影响?请你写出结论并给以证明;
(2) 如果A市受这次台风影响,那么受台风影响的时间有多长?
4.计算:
5.已知
是整数,
有两个不相等的实数根,
有两个相等的实数根,
没有实数根,求的值.
四.(1小题5分,2小题6分,共11分)
1.
解方程
2.如图(8)在ΔABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.(1)求证:ΔABC∽ΔFCD;(2)若SΔFCD=5,BC=10,求DE的长.
五.应用题(7分)
根据有关信息,有一批货物,如果本月出售,可获利100元,然后可将本利都存入银行,已知银行每月利率是0.5%;如果下月初出售,可获利120元,但要付5元的保管费,试问这批货物何时出售好?
六.(8分)
如图(9)已知⊙O1和⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AP的延长线交⊙O1于C点,BP的延长线交⊙O2于D点,直线O1O2交⊙O1于M,交⊙O2于N,与BA的延长线交于点E.
求证:(1)
;
(2)线段BC,AD分别是两圆的直径;
(3)
.
七.(9分)
如图(10)正方形OABC的顶点O在坐标原点,且OA与边AB所在直线的解析式分别为
和
,D,E分别为边OC和AB的中点,P为OA边上的一动点(点P与点O不重合),连结DE和CP,其交点为Q.
(1) 求证:点Q为ΔCOP的外心;
(2) 求正方形OABC的边长;
(3) 当ΔCOP的外接圆⊙Q与AB相切时,求点P的坐标.
参考答案:
一.填空:
1.-2300; 2.2100<375;
3.18; 4.360º; 5.47º43’36’’; 6.(1)(5);(2)(3)(4)(6); 7.
12; 8.0; 9.
;
10.
; 11.170; 12.
; 13.17; 14.4∶9; 15.2.
二.选择: 1.B; 2.A; 3.A; 4.D; 5.C.
三.
1.原式化简为
;
;
原式=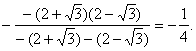
2.学校应建在AC,BD的交点处.理由:任取一点H’,用三角形两边之和大于第三边易证.
3.(1)过A作AE⊥BF,垂足是E,在RtΔABE中,∠ABE=90º-60º=30º,AB=300,
AE=AB=150<200,A市将受到这次台风影响.
(2)以点A为圆心,以200千米长为半径作弧,交BF于点C,D,在RtΔACE中,AE=150,
AC=200,
A市受这次台风影响的时间达10小时.
4.
;
5.设已知三个方程的判别式依次是Δ1,Δ2,Δ3;由题意: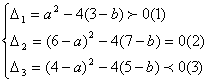
解之得:
,又
是整数,
,代人得
,
四.
1设
,则原方程化为
,即:
解之得:
.分别代人得:
,经检验都是原方程的根.
2.(1)易证∠B=∠BCE,∠ADC=∠ACB,得证ΔABC∽ΔFCD;
(2)过点A作AM⊥BC,垂足是M,
ΔABC∽ΔFCD,BC=2CD,∴
,
∵SΔFCD=5,∴SΔABC=20,又BC=10,∴AM=4;∵DE∥AM,∴
∵DM=CD=
,BM=BD+DM,BD=BC=5,∴
,∴DE=
.
五. 设这批货物的成本价为元,赢利分情况考虑如下:
若本月出售,那么到下月初共赢利
元;
若下月初出售,共赢利120-5=115元.
(1) 当
,即>2900时,本月初出售最好.
(2) 当
即=2900时,本月初或下月初出售都行.
(3) 当
即<2900时,下月初出售最好.
六.(1)∵BA切⊙O1于B,∴∠ABP=∠C,∵BA切⊙O2于A,∴∠BAP=∠D,∴ΔABC∽ΔDAB,
;
(2)过P作两圆的内公切线交AB于F,由切线长定理得:BF=PF,PF=AF,∴PF=BF=AF=AB
∴∠BPA=90º,∴BP⊥AP,∴∠BPC=∠APD=90º,∴BC,AD分别是⊙O1,⊙O2的直径.
(3)∵PF是⊙O1和⊙O2的公切线,∴PF⊥O1O2,∴∠APF=∠APE=90º,∵∠APB=90º,
∴∠ABP+∠BAP=90º,又∵PF=AF,∴∠BAP=∠APF,∴∠ABP=∠APE,∵∠E=∠E
∴ΔEPB∽EAP,
,∴.
七.(1)∵D,E分别为OC,AB的中点,∴DE∥OA,Q是CP的中点,又∵CP是RtΔCOP的斜边,∴点Q是ΔCOP的外心;
(2)由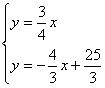
解得:
.∴点A的坐标为(4,3),∴OA=5,
正方形的边长是5.
(3)当ΔCOP的外接圆⊙Q与AB相切时,E是切点,∵AE和APO分别是⊙Q的切线和割线,
,即
,∴AP=
,∴OP=5-
.
分别作PH⊥x轴,AF⊥y轴,垂足是H,F,则PH∥AF.∴
∴
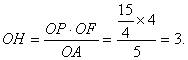PH=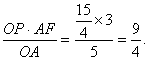
∴点P的坐标是(3,
).