第二节　整式和因式分解

知识网络

一、

二、

一、选择题

1.【05泸州】把分解因式为

　　A．　　　 B．　　  C．　 D．

2. 【05绵阳】 对x²-3x+2分解因式，结果为

A. x(x-3)+2　 　　　B. (x-1)(x-2)　 　　C. (x-1)(x+2)　 　 D. (x+1)(x-2)

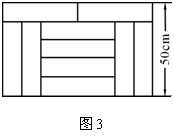3.【05绵阳】如图1，宽为50 cm的矩形图案由10个全等的

小长方形拼成，其中一个小长方形的面积为

A. 400 cm²　　　　　　 B. 500 cm²

C. 600 cm²　　　　　　 D. 4000 cm²

4.【05乌鲁木齐】下列运算正确的是

A、　　B、　　C、　　 D、

5.【05杭州】若化简的结果为,则的取值范围是:

(A)为任意实数　 (B)　 (C)　 (D)

6.【05嘉兴】下列运算正确的是（　　 ）

（A）　　　 （B）　　 

（C）　　　　 （D）

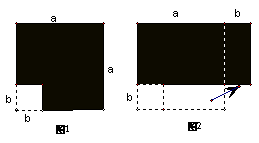
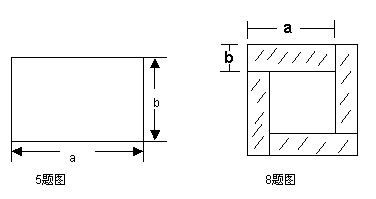
7.【05嘉兴】在边长为a的正方形中挖去一个边长为b的小正方形（a>b）（如图1），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，可以验证

（A）

（B）

（C）

（D）

8.【05丽水】把记作

（A）n　　　　（B）n＋　　　　（C）　　　　　 （D）

9.【05台州】某超市进了一批商品，每件进价为a元，若要获利25%，则每件商品的零售价应定为

（A）　　（B）　（C）　（D）

10.【05十堰课改】下列运算正确的是

A、　　B、　　C、　 D、

11.【05杭州】 “的与的和”用代数式可以表示为:　

(A)　 　(B)　　 (C)　　 (D)

12.【05武汉】某商店把一商品按标价的九折出售（即优惠10%），仍可获利20%，若该商品的标价为每件28元，则该商品的进价为（　　  ）.

（A）21元　 　 （B）19.8元　　 （C）22.4元 　　（D）25.2元

13.【05厦门】“比a的大1的数”用代数式表示是

　  A.　a＋1　　　B.　a＋1 　 C.　a　　　  D.　a－1

14.【05深圳】一件衣服标价132元，若以9折降价出售，仍可获利10%，则这件衣服的进价是

　　A、106元　　　　B、105元　　　　C、118元　　　　D、108元

15.【05玉林】因式分解4—4a+a²，正确的是(　　)．

　　A．4(1-a)+a²　 B．(2-a)²　 C．　(2-a)(2-a)　　D．　(2+a)²

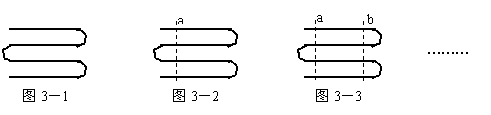16.【05河北】一根绳子弯曲成如图3－1所示的形状。当用剪刀像图3－2那样沿虚线a把绳子剪断时，绳子被剪为5段；当用剪刀像图3－3那样沿虚线b（b∥a）把绳子再剪一次时，绳子就被剪为9段。若用剪刀在虚线a，b之间把绳子再剪（n－1）次（剪刀的方向与a平行），这样一共剪n次时绳子的段数是

　　　A．4n＋1　　　　　　　　　　　B．4n＋2　　　　　　　　　　　C．4n＋3　　　　　　　　　 D．4n＋5

二、填空题

1．【05武汉】请你写出一个能分解的二次四项式并把它分解　　　　　　　　   。

2.【05常德】分解因式：a³－a=　　 　　　　　。

3.【05泰州】如下图是由边长为a和b的两个正方形组成，通过用不同的方法，计算

下图中阴影部分的面积，可以验证的一个公式是　　　　　　　　　　　  .

　　　

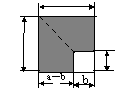4.【05无锡】分解因式：x³－x=_____　　　 ______.

5.【05锦州】如图，边长为a、b的矩形，它的周长为14，面积为10，则a²b+ab²的值为_　　　　　　　  ___. 　　　　

　

6．【05陕西】分解因式：a³－2a²b＋ab²＝__　　　　 ________。

7.【05上海】分解因式：＝　　　　　　　　

8.【05内江】如图是四张全等的矩形纸片拼成的图形，请利用图中的空白部分面积的不同表示方法，写出一个关于的恒等式　　　　　 　　　　　。

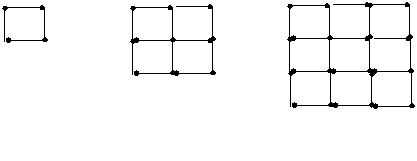
9.【05资阳】 已知n(n≥2)个点P₁，P₂，P₃，…，P_n在同一平面内，且其中没有任何三点在同一直线上. 设S_n表示过这n个点中的任意2个点所作的所有直线的条数，显然，S₂=1，S₃=3，S₄=6，S₅=10，…，由此推断，S_n=____　　　　　　　  _________.

10．【05嘉兴】分解因式：=_____　　　____________

11.【05温州】计算：2xy＋3xy＝__　　  _______。

12.【05温州】在实数范围内分解因式：ab²－2a＝___　　　　______.

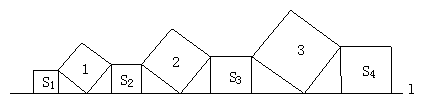
13.【05温州】在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S₁、S₂、S₃、S₄，则S₁＋S₂＋S₃＋S₄＝__　　　 _____。

14.【05十堰课改】把分解因式的结果是　 　　　　　　。

15.【05十堰课改】填上适当的数，使等式成立：　　　 =　　　。

16.【05十堰课改】代数式的三个实际意义是：　　　　　　　  、　　　　　　　　 、　　　　　　　　 。

17. 【05绵阳】若非零实数a,b满足4a²+b²=4ab，则=__　 _________.

18. 【05浙江】在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产

生的密码，方便记忆．原理是：如对于多项式，因式分解的结果是，若取x=9，y=9时，则各个因式的值是：(x－y)=0，(x+y)=18，(x²+y²)=162，于是就可以把“018162”作为一个六位数的密码．对于多项式，取x=10，y=10时，用上述方法产生的密码是：　　　　(写出一个即可)．

19．【05泸州】如图2是用火柴棍摆成边长分别是1、2、3根火柴棍时

的正方形，当边长为n根火柴棍时，若摆出的正方形所用的火柴棍的根数为S，则

S＝　　　　　　　　  　（用含n的代数式表示，n为正整数）．

20．【05丽水】下列是三种化合物的结构式及分子式，请按其规律，写出后一种化合物

的分子式　　 　　　　　　　　　．

 

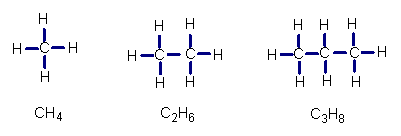
21.【05南平】因式分解：2x²-8=　　　　　　　　　  .

22.【05宁德】分解因式：x²－1＝ 　　　　　　　　 。

23.【05厦门】分解因式：5x＋5y＝　　　　　　　　　　　 .

24.【05漳州】单项式的次数是　　　　　　　　　　 。

25.【05漳州】小明在中考前到文具店买了2支2B铅笔和一副三角板，2B铅笔每支x元，三角板每副2元，小明共花了　　　　　　　　　　  元。

26.【05漳州】分解因式：＝ 　　　　　　　　　　  。

27.【05深圳】已知：，，，……，若

（a、b都是正整数），则a+b的最小值是　　　　　　　　　　　。

28.【05玉林】观察下列球的排列规律(其中●是实心球，○是空心球)：

　  ●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……

 从第1个球起到第2004个球止，共有实心球　　　　　　 个．

29.【05河北课改】分解因式1－4x²＝　　 　　　　　　　　.

30.【05河北】分解因式＝　　　　　　　　  。

31.【05河北】高温锻烧石灰石（CaCO₃）可以制取生石灰（CaO）和二氧化碳（CO₂）。

如果不考虑杂质及损耗，生产生石灰14吨就需要锻烧石灰石25吨，那么生产生石灰224万吨，需要石灰石　　　　　　　 万吨。

32.【05河北】一种药品经过两次降价后，每盒的价格由原来的60元降至48.6元，那

么平均每次降价的百分率是　　　　　　　　  。

33.【05包头】把多项式xy―x+y―1分解因式，其结果是__________________。

34.【05包头】随着通讯市场竞争日益激烈，为了占领市场，甲公司推出的优惠措施是：

每分钟降低a元后，再下调25％；乙公司推出的优惠措施是：每分钟下调25％，再降低a元。若甲、乙两公司原来每分钟收费标准相同，则收费较便宜的是_　　　　  ___公司。

35.【05毕节】一条直线上有若干个点，

点的个数	线段的条数
2	1
3	3
4	6
5	10
6	15
7

以任意两点为端点可以确定一条线段，线段的条数

与点的个数之间的对应关系如下表所示。请你探究

表内数据间的关系，根据发现的规律，填写表中

空格　　　　　　　　　   。

36.【05武汉】在同一平面上，1条直线把一个平面分成个部分，2条直线把一个平面最多分成个部分，3条直线把一个平面最多分成个部分，那么8条直线把一个平面最多分成　　　　　　　　  　　　 部分。

37.【05太原】把3x²―6x+3分解因式，其结果是____　　　　________。

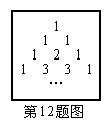38.【05泉州】我国宋朝数学家杨辉在他的著作《详

解九章算法》中提出右下表，此表揭示了（n为非负整数）展开式的各项系数的规律，例如：

，它只有一项，系数为1；

，它有两项，系数分别为1，1；

，它有三项，系数分别为1，2，1；

，它有四项，系数分别为1，3，3，1；

……

根据以上规律，展开式共有五项，系数分别为　　　　　　　　　 。

39.【05黄岗】将x – xy ²分解因式的结果是　　 　　　　　　　　 ；

40.【05黄石】分解因式：=______　　　__________。

41.【05黄石】民意商场对某种商品作调价，按原价8折出售，此时商品的利润率是10%，此商品进价为1000元，则商品的原价是______　　　　　 ______。

42.【05遂宁课改】分解因式：　　 　　　　　　　。

43.【05湘潭】如图，是2005年6月份的日历，像图中那样竖着圈住三个数。如果圈住的三个数的和为36，则这三个数

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30

中最大的数为___　　　　　　　  ___。

44.【05湘潭】观察下表：

幂运算	618	6182	6183	6184	6185	6186	6187	6188	……
结果的个位数字	8	4	2	6	8	4	2	6	……

通过以上信息，用你发现的规律得出618²⁰⁰⁵的个位数字是___　　　　　 _____。

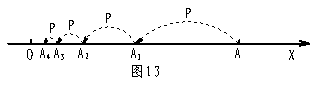
45.【05曲靖】一质点P从距原点1个单位的A点处向远点方向跳动，第一次跳动到OA的中点A₁处，第二次从A₁点跳动到OA₁的中点A₂处，第三次从A₂点跳动到OA₂的中点A₃处，如此不断跳动下去，则第n次跳动后，该质点到原点O的距离为　　　　　  。

　　　

46.【05黄岗课改】某同学在电脑中打出如下排列的若干个圆（图中●表示实心圆，○表示空心圆）：

●　　 ○●●○●●●○●●●●○●●●●●○●●●●●●○

若将上面一组圆依此规律复制得到一系列圆，那么前2005个圆中有　　　 　　个空心圆；

47.【05重庆课改】把４x＋1加上一个单项式，使其成为一个完全平方式．请你写

出所有符合条件的单项式　　　　　　　　　　　　　　．

三、解答题

1．【05南通】计算　

【解】

2.【05内江】阅读材料，大数学家高斯在上学读书时曾经研究过这样一个问题：

1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+，其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…＝？

观察下面三个特殊的等式

将这三个等式的两边相加，可以得到1×2+2×3+3×4＝

读完这段材料，请你思考后回答：

⑴ 　　　　　

⑵ 　　　　　　　　

⑶ 　　　　　　　

（只需写出结果，不必写中间的过程）

【解】⑴343400(或

⑵

⑶

3.【05青岛】（1）计算：(－2)⁰ +4×（－）．

【解】原式=1－2=－1.　

4.【05青岛】计算：2(x＋1)－x．

【解】原式=2x＋2－x= x＋2.

5.【05浙江】据了解，火车票价按“”的方法来确定．已知A站至H站总里程数为1 500千米，全程参考价为180元．下表是沿途各站至H站的里程数：

车站名	A	B	C	D	E	F	G	H
各站至H站的里程数（单位：千米）	1500	1130	910	622	402	219	72	0

例如，要确定从B站至E站火车票价，其票价为(元)．

（1）求A站至F站的火车票价(结果精确到1元)；

（2）旅客王大妈乘火车去女儿家，上车过两站后拿着火车票问乘务员：我快到站了吗？

乘务员看到王大妈手中票价是66元，马上说下一站就到了．请问王大妈是在哪一站下车的？（要求写出解答过程）．

【解】（1）154元　　（2）G站下车　　　　

6.【05杭州】宏志高中高一年级近几年来招生人数逐年增加,去年达到550名,其中面向全省招收的“宏志班”学生,也有一般普通班学生.由于场地,师资等限制,今年招生最多比去年增加100人,其中普通班学生可多招20%,“宏志班”学生可多招10%,问今年最少可招收“宏志班”学生多少名?

【解】　最少10人　　

7．【05苏州】　 苏州地处太湖之滨，有丰富的水产养殖资源，水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖，他了解到如下信息：

①每亩水面的年租金为500元，水面需按整数亩出租；

②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗；

③每公斤蟹苗的价格为75元，其饲养费用为525元，当年可获1400元收益；

④每公斤虾苗的价格为15元，其饲养费用为85元，当年可获160元收益；

  （1）若租用水面n亩，则年租金共需　　　　　　　　　  元；

　（2）水产养殖的成本包括水面年租金、苗种费用和饲养费用，求每亩水面蟹虾混合养殖的年利润(利润：收益—成本)；

　（3）李大爷现有资金25000元，他准备再向银行贷不超过25000元的款。用于蟹虾混合养殖。已知银行贷款的年利率为8％，试问李大爷应该租多少亩水面，并向银行贷款多少元．可使年利润超过35000元?

【解】（1）500n

　 （2）每亩的成本=4900

　　　　每亩的利润=3900

　 （3）李大爷应该租10亩，贷24000元。

8.【05无锡】某天，一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：

品名	西红柿	豆角
批发价（单位：元/㎏）	1.2	1.6
零售价（单位：元/㎏）	1.8	2.5

问：他当天卖完这些西红柿和豆角能赚多少钱？

【解】 33元.

9.【05丰台】分解因式：

【解】　

10.【05北京】分解因式：

【解】

　　　　 

11.【05南平】化简：3（a+5b）-2(b-a)

【解】 原式= 3a +15b – 2b + 2a=5a + 13b；

12.【05河北课改】已知，求·的值。。

【解】原式　　  当时，原式=2

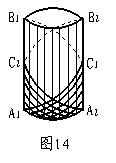
13.【05曲靖】编织一个底面周长为a，高为b的圆柱形花柱架，需用沿圆柱表面绕织一周的竹条若干根，如图14中的A₁C₁B₁,A₂C₂B_2,…则每一根这样的竹条的长度最少是　 　 。

　　　　

14.【05湘潭】先化简：(2x―1)²―(3x+1)(3x―1)+5x(x―1)，再选取一个你喜欢的数代替x求值。

【解】原式=―9x+2

选择题、填空题答案

一、选择题

1.D　　 2. B　　 3.A　　 4.D　　 5.B　　 6.D　　 7.C　　 8.C

9.C　　 10.C　  11.D　　12. A 　 13. A　 14.D　　15.B　　16.A

二、填空题

1. 2. a(a＋1)(a－1)

3.（a－b）（a＋b）=a²－b²或a²－b²=（a－b）（a＋b）

4. 　　　5. 70 　　  6．a(a－b)² 7.

8.如　　9. （或2+3+…＋n 或1+2+3+…＋n-1）

10.　　  11. 5xy　　　12. a(b＋)(b－)　　 13. 4

14.　　15. 4　 2　　　

16. 　 （长：、宽）

摩托车每辆元，自行车每辆元，辆摩托车比辆自行车贵多少钱

17. 2　　　 18. 101030等　　　　19．2n(n＋1)　　　　20．C₄H₁₀

21. 2(x+2)(x- 2)　　　 22.（x－1）(x＋1)　　　　 23. 5(x＋y)　　　 24. 5

25.（2x+2）　　 26.（a+2）(a-2)　　  27. 19　　　 28. 602

29.　　 30.(x＋y)(x－y＋a)　　　 31. 400　　　32. 10％

33. 　　 34. 乙　　 35. 21　　 36. 37　　 37. 3（x-1）²

38. 1,4,6,4,1　　　39.　　  40. (x-3y)(x+3y+2)　　41. 1375元_

42.　　 43. 19　　  44. 8　　　 45. （或（）ⁿ）

46. 446　　　　  47. －1、４x 、-4x 、4x