嵊州市2004年初三数学竞赛试题
考试时间：2004年12月19日星期日上午9:00－11:00
| 题号 | 一 | 二 | 三 | 总分 | |||
| 1－6 | 7－12 | 13 | 14 | 15 | 16 | ||
| 得分 | |||||||
一、选择题：（每小题5分，共30分）
1．小明同学买了一包弹球，其中
是绿色的，
是黄色的，余下的
是蓝色的。如果有12个蓝色的弹球，那么，他总共买了弹球 （ ）
| A.48个 | B.60个 | C.96个 | D.720个 |
2．一种儿童游戏，以确定这个人是“谁”。孩子们站成一个圆圈，并唱一首有九个单词的诗歌。按这个圆圈的顺时针方向连续计数，将第九个孩子淘汰出圈。开始时，一圈有六个孩子。按顺时针方向分别记为a，b，…，f。最后剩下的这个孩子是c。开始记数的位置是 （ ）
| A.b | B.d | C.c | D.f |
3．若
，
，则
，
的大小关系是 （ ）
| A. | B. | C. | D.不确定的 |
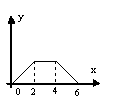
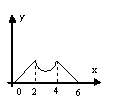
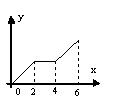
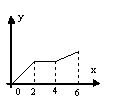
4．已知动点P在边长为2的正方形ABCD的边上沿着A－B－C－D运动，x表示点P由A点出发所经过的路程，y表示△APD的面积，则y和x函数关系的图像大致为 （ ）
|
A. |
B. |
C. |
D. |
5．如图，平行四边形ABCD中，E是AD上的一点，且AE＝
AD，对角线AC，BD交于点O，EC交BD于F，BE交AC于G，如果
ABCD的面积为S，那么，△GEF的面积为（ ）
| A. | B. | C. | D. |
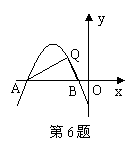6．二次函数
的图象如图所示，Q（n，2）是图象上的一点，且AQ⊥BQ，则a的值为（ ）
| A. | B. | C.－1 | D.－2 |
二、填空题（每小题5分，共30分）
7．若关于x的方程
的解为正数，则实数a的取值范围是 。
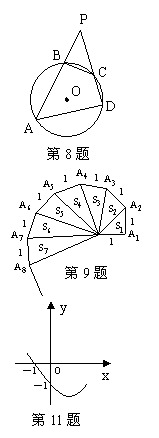8．已知四边形ABCD内接于⊙O，分别延长AB和DC相交于点P，
，AB＝12，CD＝6，PB＝8，则⊙O的面积为 。
9．观察图形，用
表示第i个三角形的面积，有
；
；
，…，若
，则n的最小值为 。
10．观察下面各组数：（3，4，5）、（5，12，13）、（7，24，25）、（9，40，41）、（11，60，61）……，发现：
，
，
……，若设某组数的第一个数为k，则这组数为（k， ，
）。
11．如图已知二次函数的图象过（－1,0）和（0,－1）两点，则化简代数式
＝ 。
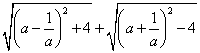12．某水池有编号为1，2，……，9的9个水管，有的是进水管，有的是出水管。已知所开的水管号与水池灌满的时间如下表，则9个水管一起开，灌满水池的时间为 。
| 水管号 | 1,2 | 2,3 | 3,4 | 4,5 | 5,6 | 6,7 | 7,8 | 8,9 | 9,1 |
| 时间（小时） | 2 | 4 | 8 | 16 | 31 | 62 | 124 | 248 | 496 |
三、解答题（每小题15分，共60分）
13．某市自来水公司，为鼓励居民节约用水，采用分段计费的方法计算水费，收费标准如表所示：
| 月用水量 | 不超过12度的部分 | 超过12度不超过 18度的部分 | 超过18度部分 |
| 收费标准(元/度) | 2.00 | 2.50 | 3.00 |
（1）小王家8月份用水20度，求应交水费多少元。
（2）小王家第二季度交纳水费情况如下：
| 月份 | 4月份 | 5月份 | 6月份 | 合计 |
| 交费金额 | 22元 | 34元 | 54元 | 110元 |
问小王家第二季度共用水多少度？
14．已知：关于x的方程①
有两个符号不同的实数根
，
，且＞
＞0；关于x的方程②
有两个有理数根且两根之积等于2。求整数n的值。
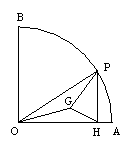
15．如图，在半径为6，圆心角为90°的扇形OAB的
上，有一个动点P，PH⊥OA，垂足为H，△OPH的重心为G。
（1）当点P在上运动时，线段GO、GP、GH中，有无长度保持不变的线段？如果有，请指出这样的线段，并求出相应的长度；
（2）如果△PGH是直角三角形，试求OG∶PG∶HG的值；
（3）如果△PGH是等腰三角形，试求出线段PH的长。
16．在密码学中，称直接可以看懂的内容为明码，对明码进行某种处理后得到的内容为密码，对于英文，人们将26个字母按顺序分别对应整数0到25，如12，4表示“me”，即“我”。现在4个字母构成的密码单词，记4个字母对应的数字分别为，，
，
。已知整数
，
，
，
除以26的余数分别为9，16，23，12，问这个密码单词是什么意思？
命题：嵊州市教研室 蔡建锋
参考答案及评分标准：
一、选择题（30分）
1.C 2.C 3.B 4.A 5.C 6.B
二、填空题（30分）
7.a＜－2 8.45π 9.n＝10 10.
，
11.
12.2小时
三、解答题（60分）
13.（1）解：
（元）··············· （6分）
（2）∵22＜12×2.00 ∴22÷2.00＝11（度）························· （3分）
∵34＞12×2.00 ∴12×2.00+（x－12）×2.50＝34
∴x＝16（度）································································· （3分）
∵54＞12×2.00＋6×2.50 ∴12×2.00＋6×2.50＋(x－18)×3.00＝54
∴ x＝23（度）
∴11+16+23＝50（度）····················································· （3分）
14．由方程①知：
∵
，＞＞0 ∴＞0，
····················· （3分）
∵△＝
∴
∴－2＜m＜2········································································· （3分）
由方程②知：
∴
∴
（舍去），
（3分）
代入②得：
∵方程的两根为有理数
∴△＝
∴△＝
∴
或
∴
或
········ （6分）
15．（1）延长HG交OP于点F ∵G是重心 ∴F为OP边中点··· （2分）
∵PH⊥OA ∴∠PHO＝90° ∴FH＝
OP＝3
∴GH＝
HF＝×3＝2···················································· （3分）
（2）延长OG交PH于点K
∵△PGH为Rt△ FG＝1，PF＝3 ∴PG＝2
∴PH＝
∴KG＝
∴OG＝
∴OG∶PG∶HG＝∶2∶2＝∶∶1············ （5分）
（3）△PGH是等腰三角形有3种可能性
①当GH＝PH时，PH＝
②当GP＝GH时，PH＝0（不存在）
③当PH＝GH时，PH＝2
∴PH＝或PH＝2·························································· （5分）
16．显然，，，都在0～25间
∵除以26余16，∴＝16或42或68
又∵是3的倍数 ∴＝42 即＝14························ （2分）
∵＝+28除以26余数为9 ∴+28＝26+9
∴＝7················································································ （2分）
∵除以26余数为12 ∴＝12或38或64
∴＝4················································································ （2分）
又∵＝+8除以26余23 ∴+8＝23或49
∴＝15·············································································· （2分）
所以＝7，＝14，＝15，＝4·································· （2分）
它们分别对应的英语字母是7－h，14－o，15－p，4－e
∴这个密码单词为hope，意思是“希望”.····························· （5分）
评分要求：
（1） 推理过于简单，得到的数正确，结论正确，得10～12分。
（2） 没有过程，只有结论，得5～7分。