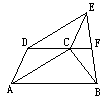例1.平面上有n条直线,它们中任意两条都不平行,且任意三条都不交于一点。这n条直线可以把平面分割成多少个部分?
此问题的变例(即特殊情况):
变例1:十刀最多可以把一张饼分成多少块?
变例2:一个圆形纸片,切100刀,最多可以将它分割为多少块?
对变例2 ,我们首先猜测其结论:
令S1,S2,……,Sn分别表示将圆形纸片切一刀,二刀,……,n刀所得块数,则有
S1 =2=1+1
S2 =4=1+1+2
S3 =7=1+1+2+3
S4 =11=1+1+2+3+4
……
Sn=1+1+2+3+4+……+n=1+![]() (n+1)·n
(n+1)·n
∴当n=100时,有S100=1+![]() (100+1)·100=5051(块)
(100+1)·100=5051(块)
解:设bn表示一条直线被n个不同的点分割后所得的分段数,则有bn=n+1.
设an-1 为平面被符合条件的n-1条直线分割成的部分数,则当平面上插入符合条件的第n条直线时,前 n-1条直线与第n 条直线相交于n-1个不同的点,这n-1个点分第n条直线为bn-1段,而每一分段恰分平面上一个已存在的部分为两个部分,于是,有:
an =an-1 +bn-1 (n>1,n∈N)
又: bn-1=n
∴ an=an-1+n=an-2+ (
n-1)+ n =……
=n+( n-1)+( n-2)+……+2+a1
又:a1=2=1+1
∴an=n+( n-1)+( n-2 )+ ……+2+1+1![]()
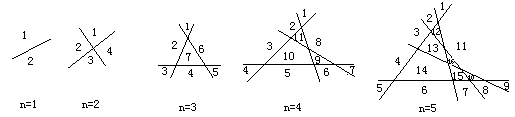
例2. 有10级台阶,小王从下向上走,若每次只能跨一级或两级,他走上去共有多少种不同的走法?
解:考虑更一般的情况:在同样条件下走n级台阶,情况如何?
设an为上n级台阶的所有不同的走法数目。若第一次走一级,则余下的n-1级有an-1 种走法;若第一次走两级,则余下的 n-2 级有an-2 种走法。
∴ an=an-1 +an-2 (n>2,n∈N)
显然a1=1,a2=2
∴a3=a1+a2=3
a4=a3+a2=5
a5=a4+a3=8
a6=a5+a4=13
a7=a6+a5=21
a8=a7+a6=34
a9=a8+a7=55
a10=a9+a8=89
思考题:用8张1×2的方格纸覆盖2×8的方格纸,共有多少种不同的覆盖方式?
解题新思路:
探究数学问题解决的新思路,对于学生发散性思维和创造性思维的培养是十分有利的。下面一道例题,是从多维度角度出发来探究解题新思路的:
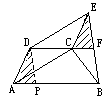
| 例:如图(1)在梯形ABCD中,AB∥CD,四边形ACED是平行四边形,延长DC交BE于F. 分析:这个题目本身不难,求证也容易,但通过对题设和结论的深入挖掘与探索,我们可以得出许多好的证法,总结如下: |
|
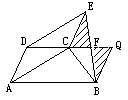
| 证明一:如图所示,作BQ∥AD,交DF延长线于Q点,则四边形ABQD是平行四边形,从而BQ=AD,再由题设可证△CEF≌△QBF, 得证EF=FB. |
|
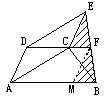
| 证明二:如左图所示:作FM∥DA交AB于M,则四边形ADFM是平行四边形,从而FM=DA.再证△CEF≌△MFB,从而结论可得证. |
|
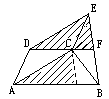
| 证明三:作CN∥EB交AB于N,则四边形CNBF是□,从而CN=FB. |
|
| 证明四:作DP∥FB交AB于P,证明△ADP≌△CEF,从而得出结论.
|
|
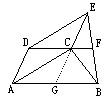
| 证明五:延长EC交AB于G,则四边形ADCG是□,∴CE=AD=GC,即C是EG中点.又CF∥GB,∴F是EB中点,结论得证. |
|
| 证明六:连结AE交CD于O点,则O 是AE中点,又OF∥AB,∴F是AB中点,得证. |
|
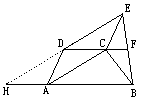
| 证明七:延长ED交BA延长线于H点,则HACD是□ , ∴CA=DH=ED ∴D是EH中点.又DF∥HB ∴F是EB中点,得证. |
|
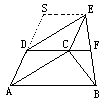
| 证明八:作ES∥CD交AD延长线于S,则CDSE是□ ∴DS=CE=AD ∴D是AS中点.又SE∥CD∥AB ∴F是EB中点,得证. |
|
证明九:在证明一作的辅助线基础上,连结EQ,则可得ECBQ是□,从而F是□ECBQ对角线EB的中点。
总之,上述不同证法的辅助线可归结为以下两种:
①作平行线构成平行四边形和全等三角形进行等量代换。
②作平行线,由题设产生中点,通过平行线等分线段定理的推论得出结论。
这其中,其实蕴含了平面几何的平移变换和旋转变换的数学思想。