初三数学竞赛专题讲座
——有关三角形与四边形的竞赛题
[例题精讲]
例1、ΔABC的面积为1，D、E为BC的三等分点，F、G为CA的三等分点（如图所示）.
求四边形PECF的面积.
例2、如图所示，A、B、C、D是一个凸四边形的四个顶点，在ABCD所在平面上求一点P，使得PA+PB+PC+PD最小.
例3、在ΔABC中，已知∠A=90º，AB=AC，BD是中线，AE⊥BD于E，延长AE交BC于F.求证：∠ADB=∠CDF.（99年天津市初中数学竞赛题）
|
例4、已知：如图，以ΔABC的AB、AC为斜边向外作直角三角形ABD和ACE，∠ADB=∠AEC=90º，且使∠ABD=∠ACE，M是BC的中点.
求证：DM=EM.（98年“祖冲之杯”邀请赛试题）
例5、已知：在ΔABC中，∠ACB=90º，∠ABC=15º，BC=1，则AC的长为（ ）
（A）2+
（B）
（C）0.3 （D）
例6、如图，P是等边三角形ABC内部的一点，PA=2，PB=
，PC=4.
求ΔABC的边长.
例7、已知：如图，边长为a的菱形ABCD中，∠DAB=60º，E是异于A、D两点的动点，F是CD上的动点，满足：AE+CF=a.
求证：无论E、F怎样移动，三角形BEF总是正三角形.
[练习题]：
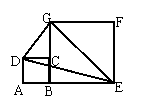1、如图，ABCD、BEFG是两个放在一起的正方形，请你证明ΔDEG的面积等于大正方形BEFG面积的一半.
2、在ΔABC中，AB=3AC.
问：（1）在ΔABC中，哪条边是最小边？
（2）
的值在什么范围内变化？
3、已知：在ΔABC中，AD为高，且AB+CD=AC+BD.
求证：AB=AC.
4、如图，AB∥EF∥CD，已知AB=10，CD=40，则EF=
.