2001年湖北省黄冈市初中数学竞赛试题
一、填空题(满分30分,每小题5分)
1.已知ｍ、ｎ互为相反数,ａ、ｂ互为负倒数,ｘ的绝对值等于3.则ｘ3-(1+ｍ+ｎ+ａｂ)ｘ2+(ｍ+ｎ)·ｘ2001+(-ａｂ)2002的值等于______.
2.已知正数ａ、ｂ,有下列命题:
(1)若ａ=1,ｂ=1,则≤1;
(2)若ａ= ,ｂ= ,则≤;
(3)若ａ=2,ｂ=3,则≤;
(4)若ａ=1,ｂ=5,则≤3.
根据以上几个命题所提供的信息,请猜想:若ａ=6,ｂ=7,则ａｂ≤________.
3.已知ｋ=== ,且+ｎ2+9=6ｎ,则关于自变量ｘ的一次函数ｙ=ｋｘ+ｍ+ｎ的图像一定经过第________象限.
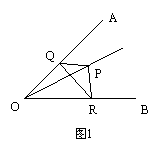4.如图1,∠ＡＯＢ=45°,角内有一点Ｐ,ＰＯ=10,在角的两边上有两点Ｑ、Ｒ(均不同于点Ｏ).则△ＰＱＲ的周长的最小值为_________.
5.某公司规定一个退休职工每年可获得一份退休金,金额与他 r工作的年数的算术平方根成正比例.如果他多工作ａ年,他的退休金比原有的多ｐ元;如果他多工作ｂ年(ｂ≠ａ),他的退休金比原有的多ｑ元.那么,他每年的退休金是(以ａ、ｂ、ｐ、ｑ表示)_________元.
6.已知在△ＡＢＣ中,∠Ａ、∠Ｂ是锐角,且ｓｉｎＡ= ,ｔgＢ=2,ＡＢ=29ｃｍ.则△ＡＢＣ的面积等于___________ｃｍ2.
二、解答题(满分70分)
7.(10分)观察:1×2×3×4+1=52,
2×3×4×5+1=112,
3×4×5×6+1=192,
……
(1)请写出一个具有普遍性的结论,并给出证明;
(2)根据(1),计算2000×2001×2002×2003+1的结果(用一个最简式子表示).
8.(10分)如图2,已知Ｒｔ△ＡＢＣ中,∠Ｃ=90°,沿过点Ｂ的一条直线ＢＥ折叠这个三角形,使点Ｃ落在ＡＢ边上的点为Ｄ.要使点Ｄ恰为ＡＢ的中点,问在图中还需添加什么条件?
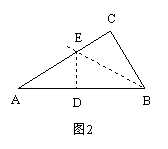(1)写出两个满足边的条件;
(2)写出两个满足角的条件;
(3)写出一个满足除边、角以外的其他条件.
9.(10分)在一次数学竞赛中,组委会决定用ＮＳ公司赞助的款购买一批奖品.若以1台ＮＳ计算器和3本《数学竞赛讲座》书为一份奖品,则可买100份奖品;若以1台ＮＳ计算器和5本《数学竞赛讲座》书为一份奖品,则可买80份奖品.问这笔钱全部用来购买计算器或《数学竞赛讲座》书,可各买多少?
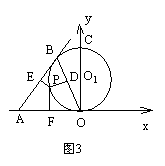10.(15分)如图3,ＯＢ是以(0,ａ)为圆心、ａ为半径的⊙Ｏ1的弦,过点Ｂ作⊙Ｏ1的切线,Ｐ为劣弧
上的任一点,且过Ｐ作ＯＢ、ＡＢ、ＯＡ的垂线,垂足分别是Ｄ、Ｅ、Ｆ.
(1)求证:ＰＤ2=ＰＥ·ＰＦ;
(2)当∠ＢＯＣ=30°,点Ｐ为的中点时,求Ｄ、Ｅ、Ｆ、Ｐ四个点的坐标及Ｓ△ＤＥＦ.
11.(10分)若ａ、ｂ、ｃ、ｄ>0,证明:在方程
ｘ2++=0;①
ｘ2++=0;②
ｘ2++=0;③
ｘ2++=0④
中,至少有两个方程有两个不相等的实数根.
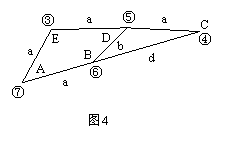
12.(15分)有麦田5块Ａ、Ｂ、Ｃ、Ｄ、Ｅ,它们的产量(单位:吨)、交通状况和每相邻两块麦田的距离如图4所示,要建一座永久性打麦场,这5块麦田生产的麦子都在此打场.问建在哪块麦田上(不允许建在除麦田以外的其他地方)才能使总运输量最小?图中圆圈内的数字为产量,直线段上的字母ａ、ｂ、ｄ表示距离,且ｂ<ａ<ｄ.
参考答案
一、1.28或-26 2.
3.三、四 4.10 5. 6.145.过点Ｃ作ＡＢ的垂线,垂足为Ｄ.∵ｓｉｎＡ==,设ｍ>0,∴ＣＤ=5ｍ,ＡＣ=13ｍ.∵ｔgＢ= =2,可设ｎ>0,ＣＤ=2ｎ,ＢＤ=ｎ,∴ＢＤ=ｎ= = ｍ.∴ＡＤ==12ｍ.从而得ＡＢ=ＡＤ+ＢＤ=12ｍ+52ｍ=292ｍ.由29=292ｍ,得ｍ=2.则ＣＤ=5ｍ=10.故Ｓ△ＡＢＣ=ＡＢ·ＣＤ=×29×10=145 (ｃｍ2).
二、7.(1)对于自然数ｎ,有ｎ(ｎ+1)(ｎ+2)(ｎ+3)+1=(ｎ2+3ｎ)(ｎ2+3ｎ+2)+1=(ｎ2+3ｎ)2+2(ｎ2+3ｎ)+1=(ｎ2+3ｎ+1)2.
(2)由(1)得2000×2001×2002×2003+1=2.
8.要使Ｄ为ＡＢ的中点,可添加下列条件之一:
角的关系:(1)∠Ａ=∠ＤＢＥ; (2)∠Ａ=∠ＣＢＥ;(3)∠ＤＥＡ=∠ＤＥＢ;(4)∠ＤＥＡ=∠ＢＥＣ;(5)∠Ａ=30°;(6)∠ＣＢＤ=60°;(7)∠ＣＥＤ=120°;(8)∠ＡＥＤ=60°.
边的关系:(1)ＡＢ=2ＢＣ;(2)ＡＣ=ＢＣ;(3)2ＡＣ=ＡＢ;(4)ＢＥ=ＡＥ.三角形的关系:△ＢＥＣ≌△ＡＥＤ.
9.设每台计算器ｘ元,每本《数学竞赛讲座》书ｙ元,这笔钱为ｓ元.则有100(ｘ+3ｙ)=ｓ=80(ｘ+5ｙ).化简得ｘ=5ｙ.解得ｓ=800ｙ.则这笔款可买《数学竞赛讲座》800本.又∵ｙ=
,∴ｓ=160ｘ.则这笔款可买计算器160台.
10.(1)提示:连结ＥＤ、ＤＦ,证△ＦＤＰ∽△ＤＥＰ;(2)Ｄ(－ａ, ａ),Ｅ(－ ａ, ａ,Ｆ(－ ａ,0),Ｐ(－ａ, ),Ｓ△ＤＥＦ= ａ2.
11.写出这四个方程的判别式Δ1、Δ2、Δ3、Δ4.注意到Δ1+Δ3>0,Δ2+Δ4>0,故Δ1、Δ2、Δ3、Δ4中至少有两个大于零,即所得四个方程中至少有两个方程有不相等的实数根.
12.设在ｘ处的最少运输量为Ｓ(ｘ).据三角形三边长度关系,有ａ+ｂ>ｄ.于是,Ｓ(Ａ)=3ａ+5(ａ+ｂ)+4(ａ+ｄ)+6ａ=18ａ+5ｂ+4ｄ;Ｓ(Ｂ)=10ａ+3ｂ+4ｄ;Ｓ(Ｃ)=18ａ+13ｄ;Ｓ(Ｄ)=14ａ+13ｂ;Ｓ(Ｅ)=26ａ+6ｂ;经比较,知ｍｉｎ{Ｓ(Ａ),Ｓ(Ｂ),Ｓ(Ｃ),Ｓ(Ｄ),Ｓ(Ｅ)}=Ｓ(Ｂ).故Ｂ处为最佳选择.