2003年全国初中数学联赛预赛暨
2002年山东省初中数学竞赛试题
一、选择题(本题共8小题,每小题6分,满分48分)
1.磁悬浮列车是一种科技含量很高的新型交通工具.它有速度快、爬坡能力强、能耗低的优点.它每个座位的平均能耗仅为飞机每个座位的平均能耗的三分之一、汽车每个座位的平均能耗的70%.那么汽车每个座位的平均能耗是飞机每个座位平均能耗的( )
(Ａ)
(Ｂ)
(Ｃ)
(Ｄ)
2.已知ａ,ｂ,ｃ,ｄ都是正实数,且<.给出下列四个不等式: ①> ②< ③> ④< 其中正确的是( )
(Ａ)①③ (Ｂ)①④ (Ｃ)②④ (Ｄ)②③
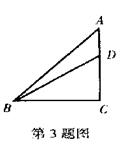
3.如图,在等腰直角三角形ＡＢＣ中,∠Ｃ=90°,∠ＣＢＤ=30°,则的值是( )
(Ａ) (Ｂ) (Ｃ)－1 (Ｄ)－1
4.世界杯足球赛小组赛,每个小组4个队进行单循环比赛,每场比赛胜队得3分,败队得0分,平局时两队各得1分.小组赛完以后,总积分最高的两个队出线进入下轮比赛.如果总积分相同,还要按净胜球数排序.一个队要保证出线,这个队至少要积( )
(Ａ)5分 (Ｂ)6分 (Ｃ)7分 (Ｄ)8分
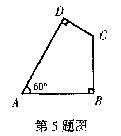
5.如图,四边形ＡＢＣＤ中,∠Ａ=60°,∠Ｂ=∠Ｄ=90°,ＡＤ=8,ＡＢ=7,则ＢＣ+ＣＤ等于( )
 |  | ||
(Ａ)6 (Ｂ)5 (Ｃ)4 (Ｄ)3
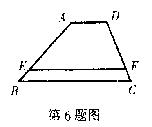
6.如图,在梯形ＡＢＣＤ中,ＡＤ∥ＢＣ,ＡＤ=3,ＢＣ=9,ＡＢ=6,ＣＤ=4.若ＥＦ∥ＢＣ,且梯形ＡＥＦＤ与梯形ＥＢＣＦ的周长相等,则ＥＦ的长为( )
(Ａ) (Ｂ) (Ｃ) (Ｄ)
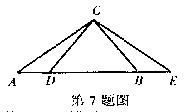7.如图,在ＲｔＡＢＣ中,∠ＡＣＢ=90°,ＡＣ=ｂ,ＡＢ=ｃ,若Ｄ、Ｅ分别是ＡＢ和ＡＢ延长线上的两点,ＢＤ=ＢＣ,ＣＥ⊥ＣＤ,则以ＡＤ和ＡＥ的长为根的一元二次方程是( )
(Ａ)ｘ2－2ｃｘ+ｂ2=0 (Ｂ)ｘ2－ｃｘ+ｂ2=0
(Ｃ)ｘ2－2ｃｘ+ｂ=0 (Ｄ)ｘ2－ｃｘ+ｂ=0
8.已知实数ａ、ｂ、ｃ满足ａ<ｂ<ｃ,ａｂ+ｂｃ+ｃａ=0,ａｂｃ=1,则( )
(Ａ)｜ａ+ｂ｜>｜ｃ｜ (Ｂ)｜ａ+ｂ｜<｜ｃ｜
(Ｃ)｜ａ+ｂ｜=｜ｃ｜ (Ｄ)｜ａ+ｂ｜与｜ｃ｜的大小关系不能确定
二、填空题(本题共4小题,每小题8分,满分32分)
9.Ｍ是个位数字不为零的两位数,将Ｍ的个位数字与十位数字互换后得另一个两位数Ｎ,若Ｍ－Ｎ恰是某正整数的立方,则这样的Ｍ共有＿＿＿＿个.
10.设ｘ1、ｘ2是方程ｘ2-2 (ｋ+1)ｘ+ｋ2+2=0的两个实数根,且(ｘ1+1) (ｘ2+1)=8, 则ｋ的值是＿＿＿＿.
11.已知实数ｘ、ｙ、ｚ满足ｘ+ｙ=5及ｚ2=ｘｙ+ｙ－9, 则ｘ+2ｙ+3ｚ=＿＿＿＿.
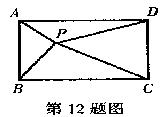
12.如图,Ｐ是矩形ＡＢＣＤ内一点,若ＰＡ=3, ＰＢ=4, ＰＣ=5, 则ＰＤ=＿＿＿＿.
三、解答题(本题共3小题,每小题20分,满分60分)
13.如图, 甲楼楼高16米, 乙楼坐落在甲楼的正北面, 已知当地冬至中午12时太阳光线与水平面的夹角为30°, 此时, 求:
(1)如果两楼相距20米, 那么甲楼的影子落在乙楼上有多高?
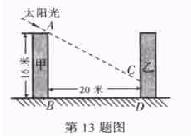(2)如果甲楼的影子刚好不落在乙楼上, 那么两楼的距离应当是多少米?
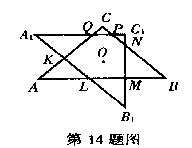
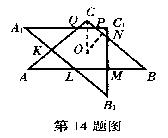
14.如图, △ＡＢＣ是等腰直角三角形,∠Ｃ=90°,Ｏ是 △ＡＢＣ内一点, 点Ｏ到△ ＡＢＣ各边的距离都等于1, 将△ＡＢＣ绕点Ｏ顺时针旋转45°得 △Ａ1Ｂ1Ｃ1, 两三角形公共部分为多边形ＫＬＭＮＰＱ.
(1)证明: △ＡＫＬ、 △ＢＭＮ、 △ＣＰＱ都是等腰直角三角形;
(2)求 △ＡＢＣ与△Ａ1Ｂ1Ｃ1公共部分的面积.
15.某乡镇小学到县城参观, 规定汽车从县城出发于上午7时到达学校, 接参观的师生立即出发去县城. 由于汽车在赴校的途中发生了故障, 不得不停车修理. 学校师生等到7时10分, 仍未见汽车来接,就步行走向县城. 在行进途中遇到了已经修理好的汽车, 立即上车赶赴县城, 结果比原定到达县城的时间晚了半小时. 如果汽车的速度是步行速度的6倍, 问汽车在途中排除故障花了多少时间.
参考解答
一、选择题
1 Ｃ 2 Ｄ 3 Ｄ 4 Ｂ 5 Ｂ 6 Ｃ 7 Ａ 8 Ａ
二、填空题
9 6 10 1 11 8 12 3
三、解答题
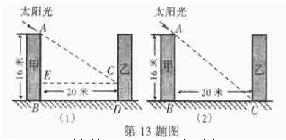13 (1)设冬天太阳最低时,甲楼最高处Ａ点的影子落在乙楼的Ｃ处, 那么图(1)中ＣＤ的长度就是甲楼的影子在乙楼上的高度.
设ＣＥ⊥ＡＢ于点Ｅ,那么在 △ＡＥＣ中,∠ＡＥＣ=90°,∠ＡＣＥ=30°,ＥＣ=20米.
∴ＡＥ=ＥＣ·ｔａｎ∠ＡＣＥ=20·ｔａｎ30°=20×≈11.6(米).
ＣＤ=ＥＢ=ＡＢ－ＡＥ=16－11.6=4.4(米).
(2)设点Ａ的影子落到地面上一点Ｃ(如图(2)),则在 △ＡＢＣ中,∠ＡＣＢ=30°,ＡＢ=16米,∴ＢＣ=ＡＢ·ｃｏｔ∠ＡＣＢ=16×ｃｏｔ30°=16×3≈27.7(米).
所以，要使甲楼的影子不影响乙楼，那么乙楼距离甲楼至少要27.7米.
14 (1)连结ＯＣ,ＯＣ1,分别交ＰＱ、ＮＰ于点Ｄ,Ｅ,根据题意得∠ＣＯＣ1=45°.
∵点Ｏ到ＡＣ和ＢＣ的距离都等于1,
∴ＯＣ是∠ＡＣＢ的平分线.
∵∠ＡＣＢ=90°,
∴∠ＯＣＥ=∠ＯＣＱ=45°.
同理∠ＯＣ1Ｄ=∠ＯＣ1Ｎ=45°,
∴∠ＯＥＣ=∠ＯＤＣ1=90°.
∴∠ＣＱＰ=∠ＣＰＱ=∠Ｃ1ＰＮ=∠Ｃ1ＮＰ=45°.
∴△ ＣＰＱ和 △Ｃ1ＮＰ都是等腰直角三角形.
∴∠ＢＮＭ=∠Ｃ1ＮＰ=45°, ∠Ａ1ＱＫ=∠ＣＱＰ=45°.
∵∠Ｂ=45°,∠Ａ1=45°,
∴ △ＢＭＮ和 △Ａ1ＫＱ都是等腰直角三角形.
∴∠Ｂ1ＭＬ=∠ＢＭＮ=90°, ∠ＡＫＬ=∠Ａ1ＫＱ=90°.
∴∠Ｂ1=45°,∠Ａ=45°,
∴ △Ｂ1ＭＬ和 △ＡＫＬ也都是等腰直角三角形.
(2)在Ｒｔ△ＯＤＣ1和Ｒｔ△ＯＥＣ中,
∵ＯＤ=ＯＥ=1,∠ＣＯＣ1=45°,
∴ＯＣ=ＯＣ1=.
∴ＣＤ=Ｃ1Ｅ=－1.
∴ＰＱ=ＮＰ=2(－1)=2－2,ＣＱ=ＣＰ=Ｃ1Ｐ=Ｃ1Ｎ=2－.
∴Ｓ△ＣＰＱ=×(2－)2=3－2.
延长ＣＯ交ＡＢ于Ｈ.
∵ＣＯ平分∠ＡＣＢ,且ＡＣ=ＢＣ,
∴ＣＨ⊥ＡＢ.
∴ＣＨ=ＣＯ+ＯＨ=+1.
∴ＡＣ=ＢＣ=Ａ1Ｃ1=Ｂ1Ｃ1=(+1)=2+.
∴Ｓ△ＡＢＣ= ×(2+)2=3+2.
∵Ａ1Ｑ=ＢＮ=(2+)－(2－2)－(2－)=2,
∴ＫＱ=ＭＮ= = ,
∴Ｓ△ＢＭＮ=×()2=1.
∵ＡＫ=(2+)－(2－)－=,
∴Ｓ△ＡＫＬ=×()2=1.
∴Ｓ多四边形ＫＬＭＮＰＱ=Ｓ△ＡＢＣ－Ｓ△ＣＰＱ－Ｓ△ＢＭＮ－Ｓ△ＡＫＬ
= (3+2)－(3－2)－1－1
= 4－2.
15 假定排除故障花时ｘ分钟.如图,设点Ａ为县城所在地,点Ｃ为学校所在地,点Ｂ为师生途中与汽车相遇之处.
在师生们晚到县城的30分钟中,有10分钟是因晚出发造成的,还有20分钟是由于从Ｃ到Ｂ由步行代替乘车而耽误的.
汽车所晚的30分钟,一方面是由于排除故耽误了ｘ分钟,但另一方面由于少跑了Ｂ到Ｃ之间的一个来回而省下了一些时间.已知汽车速度是步行速度的6倍,而步行比汽车从Ｃ到Ｂ这段距离要多花20分钟.
由此知汽车由Ｃ到Ｂ应花=4(分钟).一个来回省下8分钟,所以有ｘ－8=30,ｘ=38,即汽车在途中排除故障花了38分钟.