2003年重庆市初中数学决赛试卷（A卷）
一、选择题：
1.2003减去它的
，再减去剩余的
再减去剩余的
……依次类推，一直减去剩余的
则最后剩下的数是（
）
（A）
（B）1
（C）
（D）无法计算
2.不相等的有理数a,b,c在数轴上的对应点分别是A、B、C，如果
那么点B （ ）
（A）在A、C点的右边 （B）在A、C点的右边
（C）在A、C点之间 （D）上述三种均可能
3.在不大于2003的自然数中，既能被2除余1，又能被3除余1的数共有（ ）个。
（A）333个 （B）334个
（C）335个 （D）336个
4.若关于x的方程2x-1+a=0无解，3x-5+b=0只有一个解，4x-3+c=0有两个解，则a,b,c的大小关系是（ ）
（A）a>b>c （B）b>c>a （C）b>a>c（D）a>c>b
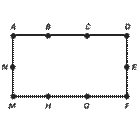
5.如图所示，长方形ADFM四周共有10个点，相邻两点之间的距离都等于1cm,以这些点为顶点构成的三角形中，面积等于3cm
的三角形共有（
）个。
（A）8 （B）9 （C）10 （D）11
6.设a、b都是整数，下列说法：（1）若 a+5b是偶数，则a-7b 也是偶数；（2）若a+b能被3整除，则a、b都能被3整除；（3）若a+b是质数，则a-b一定不是质数。上述说法中正确的个数是（ ）
（A）0 （B）1 （C）2 （D）3
7.某校图书馆有A、B、C、D四类书，借书的同学至多借3本，当m个同学任意借书后必至少有两人借的书种类、本数完全相同，则m的最小值是（ ）
（A）3 （B）15 （C）29 （D）48
二、填空题：
1如果a=2003x+2001,b=2003x+2002,c=2003x+2003,则代数式a
的值等于
。
2.一条直线上顺次有A、B、C、D、E共５个点，AB=BC-AB=CD-BC=DE-CD=1cm, 那么以这些点中的任意两个点为端点的线段中，共有 种长度。
3.现有铁矿石７３吨，计划用载重量分别为７吨和５吨的两种卡车一次运走，已知载重量７吨的卡车每台车的运费为６５元，载重量５吨的卡车每台车运费为５０元，则最省的运费是 元。
4.关于x的二次多项式a(x
,当x=2时的值是－１７，则当x=-2时，该多项式的值是 。
5.王师傅在某个特殊的岗位上工作，他每上８天班后，就连续休息２天，如果这个星期六和星期天他休息，那么，至少再过 个星期后他才能又星期天休息。
6.小明和小刚在长９０米的游泳池的对边上同时开始游泳，小明每秒游３米，小刚每秒游２米，他们来回游了１２分钟，若不计转向的时间，则他们交汇的次数是 。
7.观察数串的规律：
……，则第１００个位置上排的数是
。
三、解答题：
１.下表是某学校参加一次数学竞赛中参赛同学做对题目的情况记录表，第一行的值表示做对的题目的题数，第二行的值表示做对相应题目的同学人数。
| 做对的题数 | ０ | １ | ２ | ３ | … | １０ | １１ | １２ |
| 同学人数 | ０ | １ | ３ | ４ | … | ５ | １ | １ |
对此次竞赛的情况有如下统计：
（１）本次竞赛共有１２道题目；
（２）做对３题和３题以上的同学每人平均做对６题；
（３）做对１０题和１０题以下的同学每人平均做对５题；
问：参加本次竞赛的同学共有多少人？
2．若
b
;……。按此方法可产生一系列新数：n
……。问能否用这种方法数次，由数１０逐步产生数２００３，若能，请写出一个产生的过程；若不能，请说明理由。
参考答案：
一、选择题：
1.B 2.C 3.B 4.A 5.C 6.B 7.C
二、填空题：
1.3
2.9 3.685 4.-1 5.7 6.20
7.
三、解答题：
1.解：设共有x名同学参加了本次竞赛。
做对3题和3题以上的人数为x-(1+3)=x-4, 那么，所有同学做对
6(x-4)+1
1+23=6x-17题；
做对10题和10题以下的人数为x-(1+1)=x-2, 那么，所有同学做对
5(x-2)+111+121=5x+13题。
又做对的总题数相等，所以6x-17=5x+13.
解这个方程得 x=30.
答：共有30名同学参加了本次竞赛。
2.解：能。
因为2003=12003，可由2004=2003+1推出；
而2004=5514，可由555=551+4推出；
同理，555=1115，可由116=111+5推出；
116=429，可由33=4+29推出；
33=113，可由14=11+3推出；
14=27，可由9=2+7推出；
而9=19，可由10=1+9推出。
故可由10经7次推导后得到2003。