苍南县全国初中数学竞赛预选赛试题（有答案）

全国初中数学竞赛预选赛试题(初二)

(考试时间：120分钟，满分140分)

一、选择题：(每小题7分，共42分)

1、已知实数a满足：2004-a+＝a，那么a-2004²＝………… (　　　)

A、2003　　　　B、2004　　　 C、2005　　　D、2006

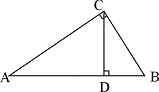2、如图，在△ABC中，∠C＝Rt∠，CD⊥AB于D，在

(1)　　 DC·AB＝AC·BC，　(2)

(3)　　   (4)AC+BC＞CD+AB

中正确的个数是 …………………………………………………… (　　　)

A、4　　　　  B、3　　　　  C、2　　　　 D、1

3、实数a，b，c，d满足：a＋b＋c＋d＝1001，ac＝bd＝4，则：

= ………………………………………… (　　　)

A、1001　　　B、2002　　　　C、2003　　　 D、2004

4、在△ABC中，∠A ＞∠B＞∠C，∠A≠90°，画直线使它把 △ABC 分成两部份，且使其中一部分与△ABC 相似，这样的互不平行的直线有( 　　)条……………………………………………………………（　　 ）

A、3　　　　　 B、4　　　　　  C、5　　　　　D、6

5、已知二次函数y=ax²+c,且当x＝1时，－4≤y ≤－1，当x＝2时,－1≤y≤5，则当x＝3时，y的取值范围是…………………………………………(　　　)

A、－1 ≤y ≤20　　　　　　　  B、 －4 ≤ y ≤15

C、7 ≤y ≤26　　　　　　　　 D、≤ y ≤

6、n是一个两位数，它的十位数字与个位数字之和为a，当n分别乘以3，5，7，9后得到四个乘积，如果其每个乘积的各位数的数字之和仍为a，那么这样的两位数有(　　)个。…………………………………………（　　　）

A、3　　　　　  B、5　　　　　  C、7　　　　  D、9

二、填空题：（每小题7分，共28分）

7、某电影院的票价是：个人每张6元，每10人一张团体票为40元，学生享

受九折优惠，某校1258名学生看电影(教师免票)，学校应向电影院至少付

_________________元钱。

8、利用公式(a²＋b²)(c²＋d²)=(ac＋bd)²＋(bc－ad)² 或其它方法找出一组正整数填空：(2²＋92×3²)(4²＋92×5²)=(　　　 ) ²+92×(　　　) ²。

9、如图，梯形ABCD的面积为34cm²，

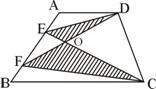AE=BF，CE与DF相交于O，△OCD

的面积为11cm²，则阴影部分的面积

为 _　　　 cm²。

10、在表达式S=中， x₁、x₂、x₃、x₄ 是1、2、3、4的一

种排列（即：x₁、x₂、x₃、x₄取1、2、3、4中的某一个数，且x₁、x₂、x₃、x₄ 互不相同）。则使S为实数的不同排列的种数有　　　　　种。

三、(本题满分20分)

某同学买某种铅笔，当他买了x支，付了y元（x、y都是整数）时，营业员说：“你要再多买10支，我就总共收你2元钱，这样相当于每买30支，你可节省2元钱”。求x·y。

四、(本题满分25分)

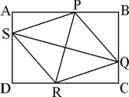如图：菱形PQRS内接于矩形ABCD，使得P、Q、R、S为AB、BC、CD、DA上的内点。已知PB=15、BQ=20、PR=30、QS=40、若既约分数为矩形ABCD的周长，求m＋n。

五、(本题满分25分)

1、试设计一种方法，把一个正方形不重复不遗漏地分割成8个正方形(分得的正方形大小可以不相同)；又问如何把正方形按上要求分成31个正方形？

2、试设计一种方法，把一个立方体分割成55个立方体(要求：不重复不遗漏，分得的立方体大小可以不相同)。

全国初中数学竞赛预选赛答案

一、1. C; 　 2.B ;　3. B; 　4. D; 　5. A; 　6. B;　

二、7. 4536;　8. 1388，2; 　9. 12;　 10. 16;

三、根据营业员的话，y的值只能是1或2。　　　　　  (3分)

(1)当y=1时，则原来每支价格为元，多买10支，每支节省元。现在每支价格为(-)元。设多买10支后共m支，则有(-)m=2……(4分)，此时m只能取15, 30, 45, 60……。经讨论只有当m=15，x=5时才符合题意。（6分）

(2)当y=2时，则(-)m=2  无论m为何整数均不合题意。　 (5分)

∴所求x=5、y=1 　　　　　　　　　　　　　　　　　　　　 (2分)

（注：y=2不讨论适当扣分）

四、设AS=x、AP=y ……(2分)，由菱形性质知PRSQ，且互相平分，这样得到8个直角三角形，易知PR与SQ的交点是矩形ABCD的中心。由已知可得其中6个三角形的边长分别为15、20、25。由对称性知CQ、CR的长为x、y。则Rt△ASP和Rt△CQR的三边长分别为x、y、25，矩形面积等于8个Rt△的面积之和。则有：

(20+x)(15+y)=6××20×15+2×xy　　　　　　 （8分）

则有  3x+4y=120　 (1)

又　　x²+y²=625 　 (2)　　　　　　　  　　　　　(2分)

得　 x₁=20　　　　　   x₂=

  　　　y₁=15　　　　　　 y₂=　　　　　　  　　　　　(5分)

当x=20时　　BC=x+BQ=40 这与PR=30不合

故  x=　　　　y=　　　　　　  　　　　　　　(2分)

∴矩形周长为2(15+20+x+y)= 　　　　　　　　　　(5分)

即：m+n=677　　　　　　  　　　　　　　　　　　　(1分)

五、

1、容易把一个正方形分成4²=16个正方形，再把其中位于一角的9个拼成一个正方形，共得：16-9+1=8个正方形 。　　　　  (8分)

分成16个正方形后，把其中任意5个分成4个小正方形，共有16-5+5×4=31个正方形。　　　　　　　　　　　　　　　　　　  (8分)

2、把立方体分割成3³=27个立方体，再把其中4个各分成2³=8个立方体，共27-4+4×2³=55个立方体。　　　　　　　　　  （9分）