2004年全国初中数学竞赛辽宁省预赛试题
一、选择题(每小题2分，共20分)
1.下列各式中，最简二次根式为--------------------------------------------( )
A.
B.
C.
D.
2.方程(x+1)x=0的根是---------------------------------------------------( )
A.x1=1，x2=0 B.x1=-1，x2=1 C.x1=-1，x2=0 D.x1=x2=0
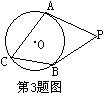
3.如图，PA、PB分别切⊙O于A、B，点C为优弧
上一点，∠ACB=60°，则∠APB的度数是--------------------------------------------------------------------(
)
A.60° B.120° C.30°或120° D.30°
4.二次函数y=-x2-4x+2的顶点坐标、对称轴分别是----------------------------( )
A.(-2,6)，x=-2 B.(2,6)，x=2 C.(2,6)，x=-2 D.(-2,6)，x=2
5.已知Rt△ABC∽Rt△A′B′C′，∠C=∠C′=90°，且AB=2A′B′，则sinA与sinA′的关系为------------------------------------------------------------------( )
A.sinA=2sinA′ B.2sinA=sinA′ C.sinA=sinA′ D.不确定
6.在下面四种边长相等的正多边形的组合中，能作平面镶嵌的组合是------------( )
7.如图，点P是x轴正半轴上的一个动点，过点P做x轴的垂线PQ交双曲线y=
于点Q，连结OQ，当点P向右运动时，Rt△QOP的面积--------------------------------(
)
A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定
8.已知⊙O1和⊙O2的半径分别为2和m，圆心距为n，且2和m都是方程x2-10x+n=0的两根，则两圆的位置关系是( )
A.相交 B.外离 C.内切 D.外切
9.将某氢氧化钠溶液加水，则描述溶液pH值与加水量(m)间变化规律的图象大致是( )
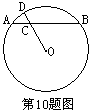
10.如图，AB是⊙O的弦，C是AB的三等分点，连结OC并延长交⊙O于点D。若OC=3，CD=2，则圆心O到弦AB的距离是--------------------------------------------------( )
A.6
B.9- C.
D.25-3
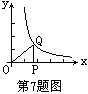
二、填空题(每小题2分，共20分)
11.已知点P(-3,2)，点P′是点P关于原点的对称点，则点P′的坐标是____。
12.如果把一个圆锥的侧面沿着它的一条母线剪开，展开在一个平面上，那么它的展开图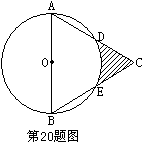
是一个____形。
13.函数
的自变量x的取值范围是_____。
14.方程组
的解是_____ 。
15.正六边形的半径为1cm，它的边心距等于_____cm。
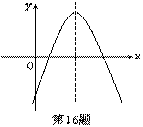
16.二次函数y=ax2+bx+c的图象如图所示，那么直线y=bx+c不经过第____象限。
17.已知圆的直径为13cm，圆心到直线l的距离为6cm，那么直线l和这个圆的公共点的个数有_____个。
18.已知5x2-xy-6y2=0，则
的值为_____。
19.△ABC内接于⊙O，D是BC边上的中点，若∠ABC+∠DAC=90°，则△ABC是____三角形。
20.如图，等边△ABC边长为10cm，以AB为直径的⊙O分别交CA、CB于D、E两点，则图中阴影部分的面积(结果保留π)是_____cm2。
三、(第21小题8分，第22小题12分，共20分)
21.当x=2时，求
的值。
22.已知线段AB是⊙O的弦，点P是优弧上一个动点(P不与A、B重合)，直线l是∠APB的平分线。
(1)画图并证明：当点P在优弧上运动时，∠APB的平分线l过定点Q；
(2)当点P在优弧上运动时，△APQ的面积能否取得最大值，如果能，请用尺规作图确定点P在⊙O上的位置；如果不能，请说明理由。
四、(10分)
23.在某文具商场中，每个画夹定价为20元，每盒水彩定价为5元。为促进销售，商场制定两种优惠方案：一种是买一个画夹赠送一盒水彩；另一种是按总价92％付款。一个美术教师欲购买画夹4个，水彩若干盒(不少于4盒)。
(1)设购买水彩数量为x(盒)，付款总金额为y(元)，分别建立两种优惠方案中的y与x的函数关系式；
(2)如果购买同样多的水彩，哪种方案更省钱？
五、(10分)
24.如图，湖心岛上有一凉亭，现欲利用湖岸边的开阔平整地带，测量凉亭顶端到湖面所在平面的高度AB(见示意图)，可供使用的工具有测倾器、皮尺。
(1)请你根据现有条件，设计一个测量凉亭顶端到湖面所在平面的高度AB的方案，画出测量方案的平面示意图，并将测量的数据标注在图形上(所测的距离用m,n,…表示，角用α,β,…表示，测倾器高度忽略不计)；
(2)根据你所测量的数据，计算凉亭到湖面的高度AB(用字母表示)。
六、(12分)
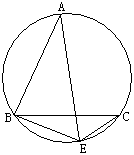
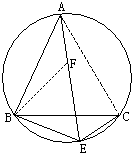
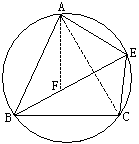
25.如图，已知A为优弧
中点，且AB=BC，E为劣弧
上一点。
(1)求证：AE=BE+CE
(2)试猜想，当点E在优弧
上运动时，线段AE、BE、CE之间具有怎样的关系，画图并证明你的猜想。
七、(12分)
26.甲、乙两辆公共汽车分别自A、B两地同时出发，相向而行。甲车行驶85千米后与乙车相遇，然后继续前进。各车到达对方的出发点等候30分钟立即依原路返回。当甲车行驶65千米后又与乙车相遇，求A、B两地距离。
八、(16分)
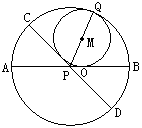
27.如图，AB、CD是半径为1的⊙P两条直径，且∠CPB=120°，⊙M与PC、PB及弧
都相切，O、Q分别为PB、弧
上的切点。
(1)试求⊙M半径r；
(2)以AB为x轴，OM为y轴(分别以OB、OM为正方向)建立直角坐标系，
①设直线y=kx+m过点M、Q，求k，m；
②设函数y=x2+bx+c的图像经过点Q、O，求此函数解析式；
③当y=x2+bx+c<0时，求x的取值范围；
④若直线y=kx+m与抛物线y=x2+bx+c的另一个交点为E，求线段EQ的长度。
参考答案
一、选择题(20分)
1.B 2.C 3.A 4.A 5.C 6.C 7.C 8.B 9.A 10.C
二、填空题(20分)
11.(3,-2) 12.扇 13.0≤x≤6，且x≠4 14.x=4，y=-1；或x=-1，y=4 15.
16.二 17.2 18.
或1 19.等腰 20.
三、
21.(8分)
解：
. …………4分
当x=2
时，
原式=
. …………4分
22.(12分)
解：
(1)图形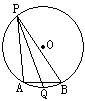
…………2分
设P是⊙O上任意点，Q为l与⊙O的交点 …………3分
∵∠APQ=∠BPQ
∴
∴Q为
中点
即∠APB的平分线过点Q …………6分
(2)能取得最大值 …………8分
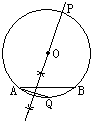…………12分
四、
23.(10分)
解：
(1)按优惠方案①可得
y1=20×4+(x-4)×5=5x+60(x≥4) …………2分
按优惠方案②可得
y2=(5x+20×4)×92%=4.6x+73.6(x≥4) …………4分
(2)比较
y1-y1=0.4x-13.6(x≥4)
令y1-y1=0，得x=34 …………7分
∴当购买34盒水彩时，两种优惠方案付款一样多。 …………8分
当4≤x<34时，y1<y2，优惠方案①付款较少。 …………9分
当x>34时，y1>y2，优惠方案②付款较少。 …………10分
五、
24.(10分)
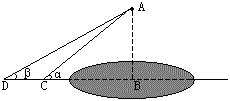解(1)如图所示，在点C测得∠ACB=α，在点D测得∠ADB=β，测得DC=m. …………4分
(2)解：在Rt△ABC中，设AB=x，BC=xcotα
在Rt△ABD中，BD=xcotβ
BD=m+BC
即xcotβ=m+xcotα
解得x=
…………10分
(注：标记字母不同，结果正确，按以上标准给分)
六、(12分)
25. (1)证明
连结AC
∵AB=BC，且点A为
中点
∴△ABC为等边三角形
在AE上截取EF=BE，连结BF
∵∠AEB=∠ACB=60°，且EF=BE
∴△EFB为等边三角形
∵∠ABC=∠FBC=60°
∴∠ABF=∠EBF
在△ABF和△CBE中
∵AB=CB
∠ABF=∠CBF
BF=BE
∴△ABF≌△CBF
∴AF=CE
∴AE=BE+CE …………6分
(2)AE=BE-CE …………8分
证明：连接AC
∵AB=BC，且A为中点
∴△ABC为等边三角形
在BE上取EF=AE，连结AF
∵∠AEF=∠ACB=60°,且EF=AE
∴△EFA为等边三角形
∵∠BAC=∠FAE=60°
∴∠BAF=∠EAC
在△ABF和△ACE中
∵AB=AC
∠BAF=∠EAC
AF=AE
∴△ABF≌△ACE
∴BF=CE
∴AE=BE-CE …………12分
七、(12分)
26.设甲车的速度为x(千米/时)，乙车的速度为y(千米/时)，A、B两地的距离为S(千米) …………2分
则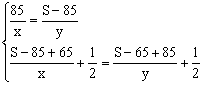
…………4分
即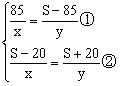
…………6分
①÷②得 
…………8分
去分母，化简得S2-190S=0 …………10分
S＝0(舍) S＝190
答：A、B两地的距离为190千米。 …………12分
八、(16分)
28.(1)由
，PM+MQ=
+r=1，得r=2
-3 …………2分
(2)①点M(0,r)=(0,2-3)，点Q(rcos60°,)即Q(
)
由已知直线过点M、Q，得
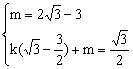
解得k=，m=2-3 …………5分
②由y=x2+bx+c过点O、Q，则
C=0
，得b=
即得
…………8分
③令
，则
，x2=0
即得当
<x<0时y<0
④由已知得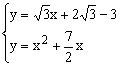
消去y得
…………12分
设点E的横坐标为x2，点Q的横坐标为
由根与系数的关系得 x2=-2
则
…………14分
进而得线段EQ的长为2+1 …………16分