2004年全国初中数学联赛试题（深圳赛区）
第一试
（时间：2004年3月13日上午9：30-11：00，满分100分）
一、 选择题（每小题4分，共40分）
1．下列几何图形中，不可能既是轴对称图形又是中心对称图形的是（ ）
A．圆； B.正三角形； C.线段； D.矩形.
2．二次函数
的图象向左平移2个单位，再向上平移3个单位，得到函数
的图象，则
的值分别为（ ）
A．6，4；
B.
； C.
；
D.
.
3．已知四边形
的两条对角线相等，但不垂直，顺次连结各边中点得四边形
，顺次连结各边中点得四边形
，以此类推，则
为（ ）
A．是矩形但不是菱形； B. 是菱形但不是矩形；
C.既是菱形又是矩形； D.既非矩形又非菱形.
4．α、β都是钝角，甲、乙、丙、丁四位同学计算
的结果依次为50°、26°、72°和90°，其中确有正确的结果，那么算得正确的是（ ）
A．甲； B.乙； C.丙； D.丁
5．使分式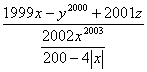
有意义的
取值范围是（ ）
A．
；
B.
； C.
； D.
6．两个物体A、B所受压强分别为
（帕）与
（帕）（、为常数），它们所受压力F（牛）与受力面积S（米2）的函数关系图象分别是射线
.如图所示，则（ ）
A．＜； B.=；
C．＞； D.≤
7．已知
、
都是有理数，且
，则
是（ ）
A．负数； B.正数； C.负数或零； D.非负数.
8．若关于的方程
的解是负数，则的取值范围是（ ）
A．
； B.
；
C.
；
D.
9．有理数
，满足：
，
，
，且
，则
的最大值是（ ）
A．1； B.2； C.3； D.5
10．在锐角△ABC中，三个内角的度数都是质数，则这样的三角形（ ）
A．只有一个且为等腰三角形； B.至少有两个且都为等腰三角形；
C. 只有一个但不是等腰三角形； D.至少有两个，其中有非等腰三角形.
二、 填空题（每小题4分，共60分）
11．2003年6月1日，举世瞩目的三峡工程正式下闸蓄水，26台机组年发电量将达到
. 用科学记数法应表示为
；
12．要使分式方程
产生增根，则
=
；
13．在Rt△ABC中，∠C=90°，
分别是∠A、∠B的对边，如果
，那么
等于 ；
14．将一个四边形的纸片一刀剪去一个角后，所得的多边形的内角之和是 ；
15．观察下列各组数：（3，4，5），（5，12，13），（7，24，25），（11，60，61）…，发现
若设某组数第一个数为
，则这个组的数为
；
16．当
时，关于的一元二次方程
有实根.
17．Rt△ABC内的点P到三边的距离均为d，斜边为c, 则直角三角形的面积为 ；
18．如果表示正方形
各边长的代数式如图所示，那么，阴影部分的面积是
 | |||||
 | |||||
 | |||||
第18题 第19题 第20题
19．在正方形ABCD中，点E是BC上的一定点，且BE=5，EC=7.
点P是BD上的一动点，则PE+PC的最小值是 .
20．如图，四边形ABCD中，已知AB∶BC∶CD∶DA=2∶2∶3∶1，且∠B=90°，
则∠DAB的度数是 ；
21．
=
；
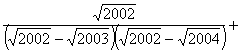
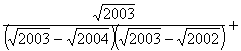
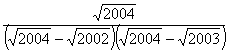22．圆的半径为5cm，其内接梯形的两底分别为6cm和8cm，则梯形的面积S= ；
23．如图所示，
是用火柴棒摆成的一序列“井”字型图案，按这种方式摆下去，当每边上摆201（即
）根时，需要的火柴棒的总根数是
根.
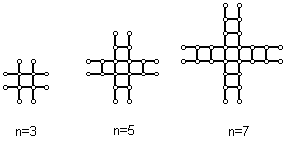
24．设
为自然数，记
，问和数1！+2！+3！+…+2003！+2004！的个位数字是
.
25．若
，且
（为常数，且
，则的取值范围是
.
答案
一、1.B 2.C 3.B 4.B 5.D 6.A 7.C 8.B 9.B 10.A
二、11．
； 12. 3 ； 13. 2：3 ； 14. 180°或360°或540°
15．
； 16.
且
17.
18.
19.13
20. 135° 21.0 22.49或7. 
24. 3 25. 