初三数学竞赛选拔试题(含答案）-初中三年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载

初三数学竞赛选拔试题

文本框: _________________学区 ___________________中学姓名_________________ 准考证号码_________________
………………………………装………………………………订………………………………线………………………………

一、选择题: (每小题5分，共 35分)

1 .2003减去它的，再减去剩余的再减去剩余的……依次类推，一直减去剩余的则最后剩下的数是（　B　）

（A）　　　　（B）1　　　　（C）　　　　（D）无法计算

2. 若 x³+ax²+bx+8有两个因式x+1和x+2，则a+b的值是 (　D　)

（A） 7　　　（B） 8　　　（C） 15　　（D）21

3. ΔABC的周长是24，M是AB的中点，MC=MA=5，则ΔABC的面积是（　C ）

（A） 12　　　（B） 16　　（C） 24　　（D）30

4. DE为∆ABC中平行于AC的中位线，F为DE中点，延长AF交BC于G，则∆ABG与∆ACG的面积比为　(　A　 )

（A）1：2（B）2：3（C）3：5（D）4：7

5. 三角形三条高线的长为3，4，5，则这三角形是（　C　）

（A）锐角三角形（B）直角三角形（C）钝角三角形（D）形状不能确定

6. 已知关于x的方程有不同的实数根，其中m为整数，且仅有一个实根的整数部分是2，则m的值为（　A　）

（A）–2（B）–3（C）–2或–3（D）不存在

7. 在凸四边形ABCD中，DA=DB=DC=BC，则这个四边形中最大角的度数是（ A　）

（A） 120º　（B） 135º　（C） 150º　（D） 165º

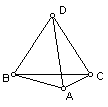
二、填空题: (每小题5分，共 35分)

1. 若在方程 y(y+x)=z+120 中， x，y，z都是质数，而z是奇数，则x=　2 .y= 11 .z= 23　.

2. 将 2003x²-(2003²-1)x-2003 因式分解得 (x-2003)(2003x+1)　　　.

3.正三角形ABC所在平面内有一点P，使得⊿PAB、⊿PBC、⊿PCA都是等腰三角形，则这样的P点有　 10　个

4.已知直角梯形ABCD中，AD∥BC，AB＝BC，∠A＝，∠D＝，CD的垂直平分线交CD于E，交BA于的延长线于F，若AD＝9，则BF＝　　9　　；

5.已知四边形的四个顶点为A（8,8），B（－4,3），C（－2，－5），D（10，－2），则四边形在第一象限内的部分的面积是　　　　　　

6.小明和小刚在长９０米的游泳池的对边上同时开始游泳，小明每秒游３米，小刚每秒游２米，他们来回游了１２分钟，若不计转向的时间，则他们交汇的次数是　20　　　。

7.一副扑克牌有54张，最少抽取　 16　　张，方能使其中至少有2张牌有相同的点数？

三、(本题满分15分)

下表是某学校参加一次数学竞赛中参赛同学做对题目的情况记录表，第一行的值表示做对的题目的题数，第二行的值表示做对相应题目的同学人数。

做对的题数	０	１	２	３	…	１０	１１	１２
同学人数	０	１	３	４	…	５	１	１

　对此次竞赛的情况有如下统计：

（１）本次竞赛共有１２道题目；

　（２）做对３题和３题以上的同学每人平均做对６题；

　（３）做对１０题和１０题以下的同学每人平均做对５题；

　问：参加本次竞赛的同学共有多少人？

解：设共有x名同学参加了本次竞赛。

　　　做对3题和3题以上的人数为x-(1+3)=x-4, 那么，所有同学做对

　　　6(x-4)+11+23=6x-17题；

　　　做对10题和10题以下的人数为x-(1+1)=x-2, 那么，所有同学做对

　　　5(x-2)+111+121=5x+13题。

　　　又做对的总题数相等，所以6x-17=5x+13.

　　　解这个方程得　 x=30.

　　　答：共有30名同学参加了本次竞赛。

四、(本题满分15分)

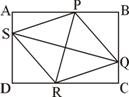如图：菱形PQRS内接于矩形ABCD，使得P、Q、R、S为AB、BC、CD、DA上的内点。已知PB=15、BQ=20、PR=30、QS=40、若既约分数为矩形ABCD的周长，求m＋n。

设AS=x、AP=y ……(2分)，由菱形性质知PRSQ，且互相平分，这样得到8个直角三角形，易知PR与SQ的交点是矩形ABCD的中心。由已知可得其中6个三角形的边长分别为15、20、25。由对称性知CQ、CR的长为x、y。则Rt△ASP和Rt△CQR的三边长分别为x、y、25，矩形面积等于8个Rt△的面积之和。则有：