华师九年级上册期末学力水平检测与评估
班级___________姓名___________ 等级___________
对号入座
1、一个人上山和下山的路程都是S，上山的速度是u1，下山的速度是u2，那么这个人上山和下山的平均速度是（ ）
A．
B .
C.
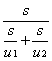D.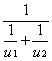
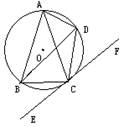
2、如图所示，ABCD内接于⊙O，AC平分∠BAD ，EF与 ⊙O 切于C， 图中与∠DCF相等的角有（ ）
A．3个 B.4个 C.5个 D.6个
3、
＝
，那么下列各式中错误的是（ ）
A 
=－7 B 
=
C 
=
D 
=
4、两圆半径分别为5和3，d为圆心距，当2＜d＜8时，这两圆的位置关系是（ ）
A 相切 B 外离 C 相交 D 内含
5、已知直角三角形的三边长分别为3、4、5，以直角边为轴旋转一周得到的圆锥的侧面积为（ ）
A 15
B 12或15
C 15或20
D 20
6、两个等圆相交于A、B两点，过B点作一直线交两圆于C、D两点，那么
△ACD一定是（ ）
A 锐角三角形 B 等腰三角形 C 直角三角形 D 钝角三角形
7、某省有7万名初中毕业生会考，为了解7万名考生的数学成绩，从中抽取1000名考生的数学成绩，进行统计分析，以下说法中正确的是（ ）
A 7万名考生是总体 B 每名考生的数学成绩是个体
C 1000名考生是总体的一个样本 D 1000名考生是样本容量
我问你答
8、空气的密度是1.239×10 –3克∕厘米，用小数把它表示出来为____________.
9、当x=3时，分式
的值等于零，则a＝_______，b≠________.
10、圆锥母线的长为5cm，高为3 cm，则侧面展开图中扇形的圆心角是______.
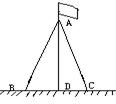
11、两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面的两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明理由。（如图）
12、甲、乙两地相距360km，新修的高速公路开通后，在甲、乙两地间行驶的长途客车平均车速提高了60%，而所用时间缩短了2h，求原来的平均速度。
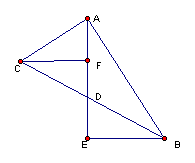
13、如图，BE⊥AE，CF⊥AE，垂足分别是E、F，D是EF的中点，△BED与△CFD全等吗？为什么？
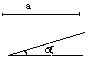
14、用尺规作图：
已知：线段a和∠
，求作：△ABC，使BC=a，∠BCA=∠。
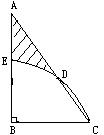
15、如图，△ABC中，∠A=30°，∠ABC = 90°，BC = 2cm,以B为圆心，BC为半径的弧交AC于D，交AB于E，求图中阴影部分的面积。
16、下图是一个寻宝游戏的示意图，宝物被随意地藏在了这个住宅内100块地板砖中某一块的下面（所有地板砖完全一样）。
| 卫生间 | 厨 房 |
| |
| 客 厅 | 饭 厅 | ||
| 卧 室 | |||
| 书 房 |
| ||
| |||
1、宝物被藏在哪个房间内的概率最大？
2、分别计算宝物被藏在6个房间内的概 率。
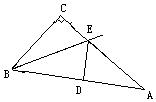
17、已知△ABC中，∠C = 90°，沿过B的一条直线BE折叠这个三角形，使点C与AB边上的一点D重合。如图所示。
（1） 要使D恰为AB的中点，还应添加一个什么条件？（请你写出三种不同的添加条件）
（2） 选择（1）中的某一个添加条件作为题目的补充条件，试说明其能使D为AB中点的理由。
解：（1）添加条件：①_____________；
②_______________；③________。
（2）说明：
18、某文化用品商场礼品专柜每天出售一种畅销的明信片500张，每张可盈利0.3元,到了年终，为周转资金减少库存，商场准备降价销售,经市场调查知道，每张明信片每降价0.1元，平均每天可多售300张，要想平均每天盈利160元，每张应降价多少元？
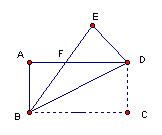19、如图，将矩形ABCD沿BD折叠，点C落在点E处，且BE交AD于F点，已知AB＜AD。
（1） 若AB = 4，BC = 8，求DF的长；
（2）
若DA平分∠EDB，求
的值。
20、某书店老板去批发市场购买某种图书。第一次购书用100元，按该书定价2.8元出售，并很快售完。由于该书畅销，第二次购书时，每本的批发价已比第一次高0.5元，用去了150元，所购数量比第一次多10本。当这批书售出
时，出现滞销，便以定价的5折售完剩余图书。问该店老板第二次售书是赔钱了，还是赚钱了（不考虑其他因素）？赔（或赚）多少钱？
《期末学力水平检测与评估》答案
1.
Ｄ ２.Ｃ ３.Ｂ ４.Ｃ 5.C 6.B 7.D
8. 0.001239克/厘米3 9.
3, -3 10.
11. 67.5km/h,解:设原来的平均速度为ukm/h,则高速公路开通后的车速为1.6ukm/h,依题意,得:
,解之得:u = 67.5,经检验u=67.5是原分式方程的解.答:原来的平均速度是67.5km/h. 13.解:△BED
≌△CFD,证明过程如下:
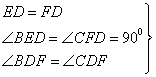
△BED
△CFD
(ASA)15.(
-
)cm２解：连结BD,在△ABC中，∠B=90°，∠A=30°，则∠DCB =
60°，所以△BCD是等边三角形，又因为BC=2cm , ∴AC=4cm,AB=AC·sin60°=2cm，∴
=
BC·AB=×2×2（cm2）,
= BC·DC·sin60°=(cm2),由扇形面积公式得
,∴
答：阴影部分的面积是（
）cm2 16.(2)客厅：P=30% 书房：P=18% 饭厅：P=12% 卧室：20%
卫生间：4% 厨房:16% 17.(1)①∠A=30°；②AB=2BC；③AC=BC；（2）∠A=
30°
D是AB的中点
18．0．1元。解：设每张应降价x元才能平均每天盈利160元，则每天可多售
·300，即3000x张，依题意得：（500+3000x）(0.3-x)=160,整理得：300x2-40x+1=0,x=
,∴x1=0.1,x2=
(不符合题意，舍去)。答：要想平均每天盈利160元，每张应降价0.1元。 19.(1)
设DF=x=BF,由勾股定理得，AF2+AB2=BF2，即（8-x）2+42=x2x=5,即DF=5；（2）∠EBD=∠CBD=
∠ADB=∠ADE；
∠ABF=∠EDF,所以∠ABF=∠FBD=∠DBC=300∠ABD=600，在△ABD中，
20.解法(一):设第二次购书x本,则第一次购书(x-10)本,依题意得:
,化简整理后,得 x2-110x+3000=0,解之得 x1=50,x2=60,经检验, x1=50,x2=60都是所列方程的根,当x=50时,每本书的批发价为150÷50=3(元),高于书的定价,不合题意舍去,当x=60时,符合题意,故第二次购书60本.(60××2.8+60×
×2.8×)-150=151.2-150=1.2(元) 答:该老板第二次购书赚了1.2元. 解法(二):设第一次购书x本,则第二次购书(x+10)本,依题意得:
,化简整理后,得x2-90x+2000=0,解之得 x1=40,x2=50,经检验 x1=40,x2=50都是所列方程的解,当x=40时,每本书的批发价为100÷40=2.5(元),第二次的批发价为2.5+0.5=3元,高于书的定价,不合题意,舍去,当x=50时,每本书的批发价为100÷50=2(元),第二次的批发价为2+0.5=2.5(元),低于书的定价,符合题意,因此,第一次购书50本,第二次购书50+10=60(本),以下同解法(一). 解法(三):设第一次购书的批发价为x元,则第二次购书的批发价为(x+0.5)元,根据题意得:
,化简整理得 2x2-9x+10=0,解之得:x1=2.5,x2=2,经检验x1=2.5,x2=2都是所列方程的根，当x=2.5时，第二次的批发价为2.5+0.5=3(元),高于书的定价,不符合题意,舍去.当x=2时,第二次的批发价为2+0.5=2.5(元),低于书的定价,符合题间.因此,第二次购书150÷(2+0.5)=60(本),以下同解法(一).