长沙市第二十九中学2005年下学期期中考试试卷
初 三 数 学
(命题：初三数学备课组 时量：120分钟 满分：120分)
一、填空题（本题共8个小题，每个小题3分，满分24分）
1、计算：
___________.
2、分式
有意义的条件是
_____________.
3、计算：
＝___________.
4、方程
的根为_______________________.
5、关于
的方程
的一个根是
，则
___________.
6、用科学记数法表示：0.000012＝_______________________.
7、直径所对的圆周角等于________度.
8、写出一个有一根为0，且另一根不为0的一元二次方程._________________.
二、单项选择题（本题共8个小题，每个小题3分，满分24分）
请将你认为正确的选择支的代号填在下面的表格里
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
9、下列各式中，是一元二次方程的是
（A）
（B）
（C）
（D）
10一元二次方程
的根为
（A）
（B）
（C）
，
（D）
，
11、给出下列各式：
，
，
，
，
，其中是分式的有
（A）5个 （B）4个 （C）3个 （D）2个
12、下列计算正确的是
（A）
（B）
（C）
（D）
13、下列各式中，属于最简分式的是
（A）
（B）
（C）
（D）
14、如果关于的方程
是一元二次方程，则
的取值为
（A）
（B）
（C）
（D）
15、下列图形中，对称轴最多的是
（A）线段 （B）正方形 （C）等腰三角形 （D）圆
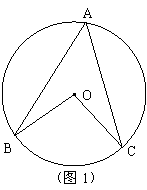
16、如图1所示，已知圆心角
，则圆周角
的度数是
（A）
（B）
（C）
（D）
三、解答题（本题共6个小题，每个小题6分，满分36分）
17、计算：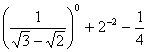
18、解方程：
19、解方程：
.
20、计算：
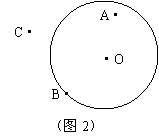
21、已知：如图2，⊙
的半径为5
，在⊙所在的平面内有A、B、C三点。
（1）点A与⊙的位置关系是______________.（2分）
（2）线段OB的长等于_________.（2分）
（3）线段OC与OB的大小关系是：OC______OB(填“＜”、“＞”或“＝”).（2分）
22、如图3，⊙的半径为5，弦AB的长为8，OC⊥AB于点C。
（1）求AC的长。（2分）
（2）求圆心O到弦AB的距离。（2分）
（3）设点P是弦AB上的一个动点，求线段OP的长的取值范围。（2分）
四、解答题（本题共2个小题，每小题8分，满分16分）
23、根据下列命题完成以下问题。
【命题】若
、
是关于的一元二次方程
的两个实数根，则有
，
。
〖问题1〗若、是关于的一元二次方程
的两个实数根，则有
____________，
___________。(2分)
〖问题2〗若、是一元二次方程
的两个实数根，则有____________，___________。(2分)
〖问题3〗甲、乙两同学解同一道一元二次方程时，甲看错了一次项系数，得两根为2和7，乙看错了常数项，得两根为1和－10。根据这些数据，你能否确定原来正确的方程？如果能，请写出原方程，并写出你的推导过程；如果不能，请说明理由。 (4分)
24、某商店10月份营业额为10万元，由于加大了宣传力度，11月份和12月份的营业额逐月增加。已知12月份的营业额为14.4万元，求该商店后两个月营业额的平均增长率。（8分）
五、解答题（本题共2个小题，每小题10分，满分20分）
25、如图4，⊙的半径为5，AB为直径，C是圆周上一点。
（1）求∠ACB的度数。（4分）
（2）若AC＝AO，求阴影部分的面积(用含
的代数式表示).（3分）
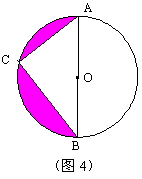（3）当C点在圆周上移动时，AC、BC、AB三条线段的长度之间存在着恒定不变的关系，请你写出一种这样的关系，并说明你的理由.（3分）
26、已知△ABC的一条边BC的长为5，另两边AB、AC的长是关于的一元二次方程
的两个实数根。
（1）求证：无论为何值时，方程总有两个不相等的实数根。（4分）
（2）为何值时，△ABC是以BC为斜边的直角三角形。（3分）
（3）为何值时，△ABC是等腰三角形，并求△ABC的周长。（3分）
长沙市第二十九中学2005年下学期期中考试
初三数学参考答案
一、填空题（本题共8个小题，每个小题3分，满分24分）
1、
2、2 3、1 4、
5、 6、
7、90 8、
（只要常数项为0即可）
二、单项选择题（本题共8个小题，每个小题3分，满分24分）
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | B | C | C | A | B | D | D | A |
三、解答题（本题共6个小题，每个小题6分，满分36分）
17、解：原式＝
18、可以用任意方法解，答案为：
19、解：方程两边同乘以最简公分母
，得………………………………………………1分
……………………………………………………………………………………3分
解这个整式方程，得
………………………………………………………………………4分
检验：将代入到最简公分母中，得
………5分
所以，是原方程的根。……………………………………………………………………6分
20、解：原式＝
＝1
21、（1）点A在⊙内 （2）5 （3）＞
22、解：（1）∵AB是⊙的弦，OC⊥AB，∴垂径定理得：AC＝
AB＝4
（2）在
中，AO＝5，AC＝4，由勾股定理得：OC＝
＝3
（3）线段OP的长的取值范围是：
四、解答题（本题共2个小题，每小题8分，满分16分）
23、〖问题1〗
；
〖问题2〗2005；-2006
〖问题3〗原来正确的方程是
………………………………………………1分
∵甲只看错了一次项系数，常数项是正确的，于是有＝14；……………………………2分
又∵乙只看错了常数项，一次项系数是正确的，于是有
………………3分
∴原来正确的方程是………………………………………………………4分
24、解：设该商店后两个月营业额的平均增长率为，根据题意列方程，得：………………1分
…………………………………………………………………………4分
解方程，得：
，
……………………………………………………6分
∵
，不合题意，应舍去。………………………………………………7分
答：该商店后两个月营业额的平均增长率为20%.……………………………………8分
五、解答题（本题共2个小题，每小题10分，满分20分）
25、解：（1）∵AB是⊙的直径，∴∠ACB＝90°
（2）∵AC＝AO＝5，∠ACB＝90°，∴BC＝
∴阴影部分S＝
（3）由三角形两边之和大于第三边，得AC+BC＞AB；
或者，由勾股定理，得
上移动时.
26、已知△ABC的一条边BC的长为5，另两边AB、AC的长是关于的一元二次方程的两个实数根。
（1）求证：无论为何值时，方程总有两个不相等的实数根。（4分）
（2）为何值时，△ABC是以BC为斜边的直角三角形。（3分）
（3）为何值时，△ABC是等腰三角形，并求△ABC的周长。（3分）
解：(1)∵
…………3分
∴无论为何值时，方程总有两个不相等的实数根。………………………………………………4分
(2)∵AB、AC的长是关于的一元二次方程的两个实数根
∴由一元二次方程根与系数的关系，得：
，
…………5分
又∵△ABC是以BC为斜边的直角三角形，由勾股定理，得：
即
∴
，整理，得：
，解得：
，
………6分
∵AB、AC是△ABC的两条边，∴AB＞0，AC＞0，∴AB+AC＞0
而当时，AB+AC＝2×（-5）＋3＝-7＜0，∴不合题意，舍去，故
∴当时，△ABC是以BC为斜边的直角三角形。……………………………………………………7分
（3）由（1）的结论可知，
，∴BC边只能是腰。……………………………………………8分
∴AB、AC中必有一边长为5，不妨设AB＝5，
也就是说关于的一元二次方程必有一根为5。
∴
，整理得：
，解得：
，
………9分
当
时，原方程为
，两根为：
，
，这时有AB＝5，AC＝4，BC＝5能构成一个等腰三角形，其周长为14。
当
时，原方程为
，两根为：
，，这时有AB＝5，AC＝6，BC＝5能构成一个等腰三角形，其周长为16。…………………………………………………………………………10分