一元二次方程测试卷 班别____姓名___________ 得分______
命题人: 江苏省如皋市九华初中 夏步俊
提示: 本卷是我自己编制的.内容涉及到一元二次方程的定义、解法、应用以及根与系数的关系.
总分100,难度系数为0.76.是一份实用性很强的试卷.
一. 填空题：（3′×8=24′）
1.
若方程
是关于
的一元二次方程，则
=_____;
2.
把方程
化为一般形式后，一次项系数是________;
3.
若
完全平方式，则的值为__________;
4.
当_______时，方程
一定有解；
5.
若
是方程
的两根，则
；
6. 以3，-5为根的一元二次方程是 ；
7.
已知
，则
＝ ；
8.
代数式
的最小值是
；
二. 选择题：（3′×8=24′）
1. 下列方程中，一元二次方程的个数有（ ）
（1）
（2）
（3）
（4）
（5）
A .1个； B.2个； C.3个； D.4个。
2.
如果代数式
的值为21，则的值一定是（ ）
A . 3 ； B. 
；C . 
；D. 
。
3．解方程
的最适当的方法应是（ ）
A．直接开平方法 B.配方法 C .公式法 D.因式分解法
4. 方程
的根是（ ）
A.
；
B.
；
C .
， D.
。
5. 以下方程中，两根和为
的是（ ）
A.
B.
C .
D.
6 .已知两个数的和为—1，积为—12，则这两个数是（ ）
A. 3和4； B. —3和4 ；C. 3和—4；D. —3和—4 。
7. 方程
的两根为
，则分解二次三项
的结果是（ ）
A . 
；B . 
；C.
； D. 
。
8. 下面是李刚同学在一次测验中解答的填空题，其中答对的是（ ）
A.
若
，则
；
B.
方程
的解是
；
C.
若分式
的值为0，则或；
D. 方程
的根的情况是原方程没有实数根。
三. 解答题：（6′×3+6′+6′+6′+6′+10′＝52′）
1. 解下列方程：（6′×3＝18′）
（1）
（2）
（3）
2.
把二次三项
分解因式。（6′）
3.
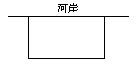
某养殖场要围成一个面积为150㎝
的长方形鱼池，如图，鱼池的一边利用河岸，另三边用鱼网围圈，如果鱼网的长为35，求鱼池的长和宽。（6′）
4.
已知
并且
﹥0，求
的值。（6′）
5.
已知方程
的两个根是一个直角三角形的两条直角边的边长，求这个直角三角形斜边的长。（6′）
6.
已知关于的方程
有两个相等的实数根。（10′）
（1）
求
的值；（4′）
（2）
若满足方程
，试判断方程的根的情况，若方程有实数根，请求出它的实数根；若方程没有实数根，请说明理由。（6′）
附答案：
一.填空题：
1.-1；2.-5；3.
；4.
；5.
；6.
；7.3；8.
。
二.选择题：
1.A; 2. B; 3. D; 4.D; 5.C; 6.C; 7.B; 8.D.
三. 解答题：
1.（1）
；（2）
；（3）
；2.
或
3.长为15，宽为10或长为20，宽为
；4.当
时，
；
舍去；
5.
；
舍去。6.（1）
；（2）当
时，原方程变形为
，此时△＞0，方程有两个不相等的实数根；当时，原方程变形为
，此时△＜0，方程没有实数根。
E-mail 2005.10.21