2006年浙江省基础教育课程改革省级实验区初中学业水平考试调研
数 学
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 合计得分 |
| 得分 |
说明：
1．本调研卷在于了解我省课程改革实验区学生的学业及试题的难度情况．请您认真作答，感谢您的支持！
2．本调研卷共4页，有3大题12小题，满分75分．测试时间60分钟．
参考公式：二次函数y=ax2+bx+c的顶点坐标是
．
一、选择题（本题有5小题，每小题4分，共20分，请选出各题中一个符合题意的正确选项，不选、多选、错选均不给分）
1．若a≠0，则下列运算正确的是（ ）
(A)
(B)
(C)
(D)
2．若反比例函数
的图象经过点（－3，2），则
的值是（ ）
（A）
（B）
（C）5 （D）6
3．随机抽查某商场四月份中5天的营业额分别如下（单位：万元）
3.4 2.9 3.0 3.1 2.6
估计这个商场四月份的营业额大约是（ ）
（A）90万元 （B）450万元 （C）3万元 （D）15万元
4．如图，等腰Rt△ABC绕C点按顺时针旋转到△A1B1C1的位置（A，C，B1在同一直线上），∠B=90º，如果AB=1，那么AC运动到A1C1所经过的图形面积是（ ）
（A）
（B）
（C）
（D）
5．如图所示，一块直角三角板ABC（∠A=30º）的斜
边AB与一个以r为半径的圆轮子相靠，若BD＝1，
则r等于（ ）
（A）2 （B）
（C）1.5 （D）
二、填空题（本题有3小题，每小题5分，共15分）
6．分解因式：a3－4a2b+4ab2＝ ．
7．对于平行四边形ABCD，给出下列五个条件：①AB=BC；②AB⊥BC；③AC=BD；④AC⊥BD；⑤BD平分∠ABC．其中要使该平行四边形成为正方形必须同时满足的两个条件是 （只要填写两个你认为合适条件的编号）．
8．以下的（1）（2）两题，每个考生只须选答一题，如果两题都答，只以第（1）题计分[第（1）题答对得5分；第（1）题不答，第（2）题答对得3分]．
（1）有2张大小、形状都相同但画面不同的长方形图片，将每张图片剪成大小、形状相同的两部分，这样就得到4张画面不完整的图片．洗匀后闭上眼睛从中取出2张，恰好能拼成一张完整图片的概率是 ．
（2）从1到9这9个自然数中任取一个数，所取的这个数是2的倍数的概率是 ．
三、解答题（本题有4小题，共40分）以下各小题必须写出解答过程．
9．（本题8分）
解不等式组：
 |
10．（本题8分）
如图，四边形A1B1C1O，A2B2C2C1，A3B3C3C2均为正方形．点A1，A2，A3和点C1，C2，C3分别在直线
和x轴上．求点C1和点B3的坐标．
11．（本题12分）
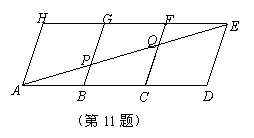如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，
(1) 若AB=6，求线段BP的长；
(2) 观察图形，是否有三角形与△ACQ全等？并证明你的结论．
12．（本题12分）
现有边长为120 cm的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
（1）小明认为，在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．于是他对水槽的横截面设计了如下两种方案：
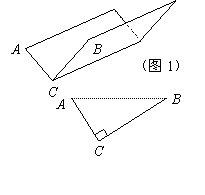
方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x (cm)，该水槽的横截面面积为y (cm2)，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值是多少？
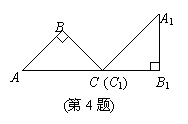
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．
（2）请你再提供两种方案，使你所设计的水槽的横截面面积比小明设计的更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．
 |
