点动型探究题2006.1.22
一.点在直线上运动
(1)(2005年北京市)
如图所示，一根长2a的木棍(AB)，斜靠在与地面（OM）垂直的墙（ON）上，设木棍的中点为P. 若木棍A端沿墙下滑，且B端沿地面向右滑行.
（1）请判断木棍滑动的过程中，点P到点O的
距离是否变化，并简述理由.
（2）在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？简述理由，并求出面积的最大值.
（2）、（2005年无锡市）
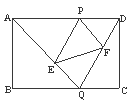
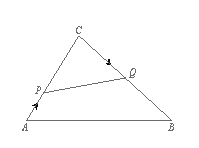
如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.
（1）求证：△APE∽△ADQ；
（2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？
（3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）
二.直角坐标系中的动点
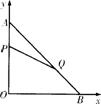
（3）．（重庆市2005）如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒．
(1) 求直线AB的解析式；
(2) 当t为何值时，△APQ与△AOB相似？
(3) 当t为何值时，△APQ的面积为
个平方单位？
练习
1.（分类讨论题）
已知：如图，△ABC中，∠C＝90°，AC＝3厘米，CB＝4厘米．两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动．当点Q运动到点A时，P、Q两点运动即停止．点P、Q的运动速度分别为1厘米/秒、2厘米/秒，设点P运动时间为
（秒）．
（1）当时间
为何值时，以P、C、Q三点为顶点的三角形的面积（图中的阴影部分）等于2厘米2；
（2）当点P、Q运动时，阴影部分的形状随之变化．设PQ与△ABC围成阴影部分面积为S（厘米2），求出S与时间的函数关系式，并指出自变量的取值范围；
（3）点P、Q在运动的过程中，阴影部分面积S有最大值吗？若有，请求出最大值；若没有，请说明理由．
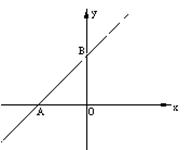
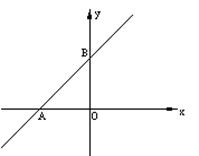
2．如图，已知直线y=x+4与x轴、y轴分别相交于点A、B，点M是线段AB(中点除外)上的动点，以点M为圆心，OM的长为半径作圆，与x轴、y轴分别相交于点C、D．
（1）设点M的横坐标为a，则点C的坐标为 ，点D的坐标为 （用含有a的代数式表示）；
（2）求证：AC=BD；
（3）若过点D作直线AB的垂线，垂足为E．
①求证： AB=2ME；
②是否存在点M，使得AM=BE？若存在，求出点M的坐标；若不存在，请说明理由．
