练3、解：(1)证明:∵直线y=x+4与x轴、y轴相交于A、B两点
∴OA=OB=4 又∵直线x=4经过点（4，0）且垂直于x轴
即直线AN经过A点，且垂直于OA ∴AN为半圆D的切线
|
∴AN∥OB
|
|
|
|
|
又∵OM、MN、NA均为半圆D的切线
|
|
|
|
|
|
|
∴∠1=∠2= 
∠OMN，∠MND=∠AND=∠3
|
|
∴∠2+∠MND=90° 则∠MDN=90°
|
∴∠4+∠MD0=90°而∠1+∠MD0=90°
∴∠1+∠4 即∠0MD=∠ADN
（2）解：由△DNO∽△NDA可得， 
=
即
=
∴y与x的函数解析式为y= 
(0﹤x﹤4)
(3)解：当以A、F、N为顶点的三角形与△ADE相似时，则有：
①若∠3=∠AED
在Rt△DNA中∠4+∠3=90°（1） 在△AEDK，∠4+∠AED=135°（2）
由（2）-（1）可得，∠AED=∠3=90°
∴MN平行于是x 轴，此时y=x=2 ∴直线NM的解析式为y=2
②若∠3=∠4
在Rt△DNA中∠4+ ∠3=90° 即2∠4+∠3=180°
∴∠3=∠4=60° 在Rt△DNA中,y=AN=AD·tan60°=2
将y值代入解析式得x= 
∴M点坐标为（0，），N点坐标为（4，2）
由M、N两点的坐标求得直线MN的解析式为y=
x+
∴直线MN的解析式为y=2或 y=x+
练2解． （1）BE=AD………………………………………………………………1分
证明：∵△ABC与△DCE是等边三角形
∴∠ACB=∠DCE=60° CA=CB，CE=CD…………………………………2分
∴∠BCE=∠ACD ∴△BCE≌△ACD……………………………………3分
∴ BE=AD…………………………………………………………………4分
（也可用旋转方法证明BE=AD）
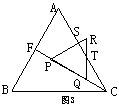
（2） 如图在△CQT中 ∵∠TCQ=30° ∠RQT=60°
∴∠QTC=30° ∴∠QTC=∠TCQ
∴QT=QC=x
∴ RT=3－x ……………………………………5分
∵∠RTS＋∠R=90° ∴∠RST=90°…………………………………………6分
∴y=
×32 －
(3－x)2=－(3－x)2＋
(0≤x≤3) ……………10分
（不证明∠RST=90°扣2分，不写自变量取值范围扣1分）
（3）C′N·E′M的值不变 ……………………………………………………11分
证明：∵∠ACC′=60°∴∠MCE′＋∠NCC′=120°
∵∠CNC′＋∠NCC′=120° ∴∠MCE′=∠CNC′ ……………………12分
∵∠E′=∠C′ ∴△E′MC∽△C′CN
∴
∴C′N·E′M=C′C·E′C=
×=
………………14分
练1解、在Rt△PMN中，∵PM＝PN，∠P＝90°，
∴∠PMN＝∠PNM＝45°，
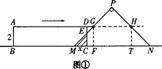
延长AD分别交PM、PN于点G、H，过点G作GF⊥MN于F，过点H作HT⊥MN于T，∵DC＝2cm，∴MF＝GF＝2cm，TN＝HT＝2cm，
∵MN＝8cm，∴MT＝6cm，
因此，矩形ABCD以每秒1cm的速度由开始向右移动到停止，和Rt△PMN重叠部分的形状可分为下列三种情况：
（1）当C点由M点运动到F点的过程中（
，如图①所示，设CD与PM交于点E，则重叠部分图形是Rt△MCE，且MC＝EC＝x，∴
（）
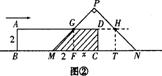
（2）当C点由F点运动到T点的过程中（
），如图②所示，重叠部分是直角梯形MCDG，∵MC＝x，MF＝2，∴FC＝DG＝x－2，且DC＝2，∴
（）；
（3）当C点由T点运动到N点的过程中（
），如图③所示，设CD与PN交于点Q，则重叠部分是五边形MCQHG，∵MC＝x，∴CN＝CQ＝8－x，且DC＝2，
∴
（）。
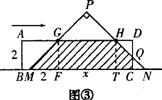
练424绵阳市2005年.
(1) 当点P运动2秒时，AP=2 cm，由∠A=60°，知AE=1，PE=
.
······················································································································································ 2分
∴ SΔAPE=
. ·························································································································· 4分
(2) ① 当0≤t≤6时，点P与点Q都在AB上运动，设PM与AD交于点G，QN与AD交于点F，则AQ=t，AF=
，QF=
，AP=t+2，AG=1+，PG=
.
∴ 此时两平行线截平行四边形ABCD的面积为S=
. ······································· 8分
当6≤t≤8时，点P在BC上运动，点Q仍在AB上运动. 设PM与DC交于点G，QN与AD交于点F，则AQ=t，AF=，DF=4-，QF=，BP=t-6，CP=10-t，PG=
，
而BD=
，故此时两平行线截平行四边形ABCD的面积为S=
.
······················································································································································ 10分
当8≤t≤10时，点P和点Q都在BC上运动. 设PM与DC交于点G，QN与DC交于点F，则CQ=20-2t，QF=(20-2t)，CP=10-t，PG=.
∴ 此时两平行线截平行四边形ABCD的面积为S=
.
······················································································································································ 14分
故S关于t的函数关系式为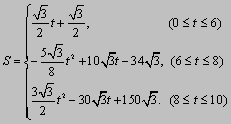
②(附加题)当0≤t≤6时，S的最大值为
；··································································· 1分
当6≤t≤8时，S的最大值为
；······················································································· 2分
当8≤t≤10时，S的最大值为；····················································································· 3分
所以当t=8时，S有最大值为 . ······················································································ 4分
(如正确作出函数图象并根据图象得出最大值，同样给4分)