2006年学能考试（一模）参考答案
一．选择题 (每小题3分, 共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | A | D | D | B | D | D | A | C |
二．填空题（每小题4分，共24分）
11． 6 12．
2 13． 10 14． 
15． 4 16． 2或2
三.解答题(本大题有8个小题，共66分)
17．(本题6分)
解：构造一个一元二次方程正确…… 3分 求其根正确…… 3分
18、(本小题满分6分)
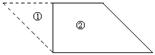
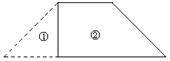
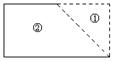
解：拼成的图形为：（每图2分，共6分）
（1）矩形，最大边长为2；（2）等腰梯形，最大边长为3；（3）平行四边形，最大边长为2。
19．(本小题满分6分)
（1）
, 
……… 2分
（2）
… 1分
x－1=n 或n+1 ， 所以x1=n+1，x2 =n+2 …… 2分 检验……… 1分
20、(本小题满分8分)
（1）画图略… 4分（不用圆规画60°扣2分，可画正三角形或轴对称法得到60°角）
（2）
， 即点A旋转过程中所经过的路程为
…………4分
21、(本小题满分8分)
（1）m=0.20， n=21；…… 4分（各2分） （2）补全频率分布直方图；…… 2分
（3）“众数”、“中位数”均在80.5—90.5组内………… 2分（对1个得1分）
22、(本小题满分8分)
解：（1）解法一：连结AB，
⌒ ⌒ ⌒ ⌒
--------2分
…… ……2分
（ 解法二：连结OC，OD，证明△AOC≌△BOC ------4分 ）
（2）四边形AOBM是菱形，……1分
理由如下：∵BM∥OA ∴∠OAM＋∠AMB＝180°……1分
又∵∠OAM＝∠OBM ∴∠OBM＋∠AMB＝180°……1分
∴OB∥AM ∴四边形AOBM是平行四边形-------1分∵OA=OB ∴四边形AOBM是菱形
23、(本小题满分12分)
（1）y=30+b； y=30+b+c（x－a）………各2分 共4分
（2）①
由此得：c=3，3a－b=45
假设a＜12，则30+b+3（12－a）=33 得 3a－b=33 这与3a－b=45 矛盾
∴a≥12，故30+b=33， ∴b=3， ∴a=16 …………3分（a 、b 、c各1分 ）
（注：若不讲理由就从30+b=33，得b=3要扣1分）
 |
|
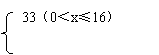②只要满足条件的方案即可，如方案：分成16、16、23，托费120元。………3分
（方案2分， 托费120元1分）
24、(本小题满分12分)
解：（1）设二次函数解析式是
，把（0，0）代入得
，
解得
，∴二次函数解析式为
…………2分
令
得
解得，
∴
∵四边形ABCD是正方形，∴
∴
∴C（12，4），
∴D（8，8） ----------2分
（2）设平移后的解析式为
，把C（12，4）代入并解得k=16，
∴平移后二次函数的解析式是+16， --------1分
当
时，y=16 ∴点D（8，8）不在此二次函数的图象上，------1分
∴不能将二次函数图象沿直线
平移后同时经过点C，D。…………1分
(同样，若把点D（8，8）代入平移后的解析式，解得k=8，则点C（12，4）不在……)
（3）① r=2 ， ② r=6 ------------各1分
③ 当
时，圆上不存在点到BD的距离为2；√
当
时，圆上有1个点到BD的距离为2；
当
时，圆上有2个点到BD的距离为2；√
当
时，圆上有3个点到BD的距离为2；
当
时，圆上有4个点到BD的距离为2 √
（③共3分，三个√各1分）