2005学年第一学期期末检测试卷
初三数学参考解答和评分标准
一．选择题(每题3分,共45分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | D | D | C | C | B | D | C | A |
二.填空题(每题4分,共20分)
11. 
12. 21 13. 写内切或外切得4分，写相切得2分
14. 1500 15. 答案不唯一，例如：
16. 11
三.解答题(共55分)
17. 评分标准：每小题4分；图形正确，但无作图痕迹，得2分；方法正确，但图形有明显误差，得3分.
18. （1）
= 
………（2分）
= －1 ………（2分）
（2）
=
……（2分）= 
………（2分）
（3）
= 
= 
……………（2分）
= 
………（1分） =
…………（1分）
（4）原式=
…………………（1分）
=
………（1分）
=
…………（1分）
=
………（1分），
当x=－1时，原式=
…………（1分）
19．（1） 
…………………………（2分）
…………（2分），
，
…………（1分）
（2）
，
，
……………………………（1分）
……………………………（1分）
所以
……………………………（2分）
原方程的解为：
，
……………………………（1分）
注：用因式分解法得出方程的解，也得满分.
（3）由题意，得
…（3分） 解得 
……（2分）
注：方法不限，其它方法求得结果，也得满分
20．写出结论：∠BDA=60º(或∠CDA＝60º)……（2分）
完成证明过程，再得……（3分）
21．（1）证明：∵□ABCD ，∴ AB∥CD且AB=CD…………………（1分）
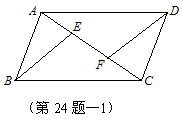∴∠BAE
=∠CDF…………………（1分）
在△ABE和△CDF 中
∵ AB=CD，∠ABE =∠CDF，AE=CF
∴ △ABE ≌ △CDF …………………（1分）
∴ BE=DF．…………………（1分）
（2）证明：∵BF∥AC，
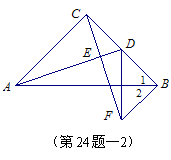∴∠CBF+∠BCA =180º，又∵∠BCA =90º，
∴∠CBF=∠BCA =90º ……………（1分）
∵AC=BC，∴∠1=∠BAC=45º=∠2 ………（1分）
又∵CE⊥AD，
∴∠CAD+∠ACE =∠BCF+ ∠ACE =90º,
∴∠CAD=∠BCF ……………（1分）
在△ACD和△CBF 中 ∵∠CAD=∠BCF，AC=BC，∠CBF=∠BCA，
∴ △ACD≌ △CBF ∴CD=BF …………………（1分）
又∵D为BC的中点，∴BD=CD=BF ……………（1分）
∴AB垂直平分DF. …………………（1分）
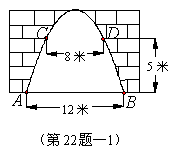
22. 如图，由题意可知各点的坐标，A(-6,0),B(6,0),C(-4,5),D(4,5)，由于顶点在y轴，可设抛物线的解析式为
， 将点A(-6,0), D(4,5)的坐标代入，得方程组 
……（2分） 解得
，
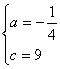……（2分）
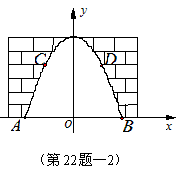所以，门洞的高度是9米. …………………（2分）
23．设初一年级每小时走
千米， …………………（1分）
由题意得
………（2分） 解得=5 …………（1分）
经检验，=5是原方程的解…………………（1分）
答：初二每小时走6千米，初一每小时走5千米. …………………（1分）
24．解：（1）相交 …………………（3分）
（2）设顶点P的坐标为（，
），则它只能是抛物线的最高点或最低点…（1分）
由题意知：1＜＜3，且
经过点A（0，1），所以点P的位置高于点A，说明点P不是抛物线的最低点，所以，点P是抛物线的最高点. …（2分）
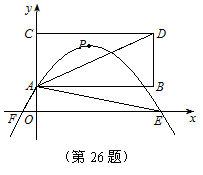由此可判断：
抛物线的开口向下. ……（1分）
（3）如图，设抛物线与轴的交点坐标为
F（
，0）、E（
，0），则＜0，＞0
S△AEO=
OE•OA= ；
S△AFO=OF•OA=
…………（1分）
∵S△AEO－S△AFO = 3 ∴ －（）=3 ，即+=6
∵+=
+
=
∴ = 6 ，即
……① …………（1分）
另一方面，设直线AD的解析式为
，并把点A（0，1）、D（4，3）的坐标代入解析式得
，解得
，∴ 
由于抛物线与线段AD有一个交点的横坐标为
，所以纵坐标=
把点（，
）的坐标代入，
整理得
……②
……………………（1分）
解由①②组成的方程组得 
，
…………（1分）