2006年中考数学第一次模拟试题
友情提醒：请将所有答案或答题过程写到答题卡上（另纸）。
一、选择题（每小题3分，共30分）
1、
的值是（ ▲ ）
A、－3 B、3 C、9 D、－9
2、下列图形既不是轴对称图形也不是中心对称图形的是（ ▲ ）
A、 等边三角形 B、平行四边形 C、直角梯形 D、菱形
3、下列计算中，正确的是（ ▲ ）
A、
B、
C、
D、
4、已知两圆半径分别为2cm和3cm，当两圆外切时，它们的圆心距d满足（ ▲ ）
A、
B、
C、
D、
5、已知菱形的边长为6，一个内角为60°，则菱形较短的对角线长是（ ▲ ）
A、6 B、
C、3 D、
6、如果x>0，那么下列函数中，y随x的增大而减小的是（ ▲ ）
A、
B、
C、y=x－1 D、
7、某校九（3）班的全体同学喜欢的球类运动用如图所示的统计图来表示，下面说法正确的是（▲ ）
A、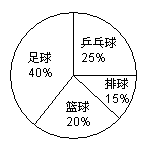 
从图中可以直接看出喜欢各种球类的具体人数；
B、 从图中可以直接看出全班的总人数；
C、 从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况；
D、从图中可以直接看出全班同学喜欢各种球类人数的大小关系。
8、函数
的自变量x的取值范围是（ ▲ ）
A、
B、
C、
D、
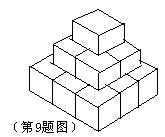9、一个画家在地面上把14个边长为1m的正方形，摆成如图的形式，然后他在露出的表面涂上颜色，那么被他涂上颜色的面积有（ ▲ ）
A、21 B、24 C、33 D、37
10、2004年6月3日中央新闻报道，为鼓励居民节约用水，北京市将出台新的居民用水收费标准：①若每月每户居民用水不超过4立方米，则按每立方米2元计算；②若每月每户居民用水超过4立方米，则超过部分按每立方米4.5元计算（不超过部分仍按每立方米2元计算）。现假设该市某户居民某月用水x立方米，水费为y元，则y与x的关系用图象表示正确的是（ ▲ ）
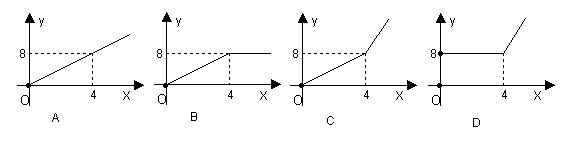
二、填空题（每小题3分，共15分）
11、口袋中放有3只红球和6只黄球，这两种球除颜色外没有任何区别。随机从口袋中任取一只球，取到黄球的概率是 ▲ 。
12、已知A点的坐标是（2，－2），A＇点是它关于原点的对称点，则A＇点的坐标是 ▲ 。
13、请你写出互为补角的两个角的度数 ▲ 。
14、苹果的零售价格是每千克5元，一次购买10千克以上按批发价，批发价格是零售价格的8折，买15千克苹果应该付 ▲ 元。
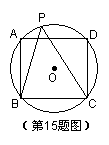
15、已知正方形内接于⊙O，P是劣弧AD上任意一点（如图），
则∠ABP+∠DCP＝ ▲ 。
三、解答题（每小题6分，共24分）
16、解不等式组
17、已知方程
18、先化简，再求值：
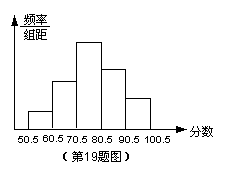19、某班同学参加环保知识竞赛，将学生的成绩(得分取整数)进行整理后分成五组，绘成频率分布直方图。图中从左到右各小组的小长方形的高的比是1∶3∶6∶4∶2，最右边一组的频数是6。结合直方图提供的信息，解答下列问题：
| |
⑵成绩落在哪组数据范围内的人数最多，是多少？
⑶求成绩在60分以上（不含60分）的学生占全班参赛人数的百分率。
四、每小题7分，共14分。
20、已知一次函数
当x=2时y的值为－3。
|
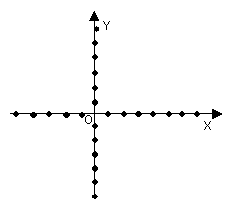
⑵在直角坐标系内画出这个函数的图象。
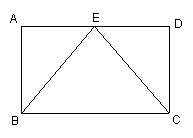
21、已知：如图，在矩形ABCD中，E是AD边上一点，
且BE＝CE。求证：AE＝DE.
|
五、每小题8分，共16分。
22、已知一个二次函数图象的对称轴是x=1，且经过（－1，4）、（0，
）两点，求这个二次函数解析式。
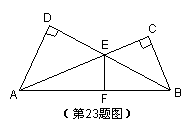
23、如图，在△ABD与△ABC中，∠C＝∠D＝90°。BD与AC相交于点E，EFAB于F。
求证：AC·AE+BD·BE＝AB2
六、本题共10分。
24、如图①，一个无盖的正方形盒子的棱长为10厘米，顶点C1处有一只昆虫甲，在盒子的内部顶点A处有一只昆虫乙.（盒壁的厚度忽略不计）
⑴假设昆虫甲在顶点C1处静止不动，如图①，在盒子的内部我们先取棱BB1的中点E，再连结AE、EC1。昆虫乙如果沿路径A→E→C1爬行，那么可以在最短的时间内捕捉到昆虫甲。仔细体会其中的道理，并在图①中画出另一条路径，使昆虫乙从顶点A沿这条路径爬行，同样可以在最短的时间内捕捉到昆虫甲。（请简要说明画法）
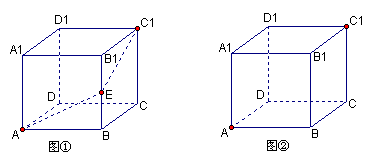⑵如图②，假设昆虫甲从顶点C1，以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行，同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？（精确到1秒）
七、本题11分。
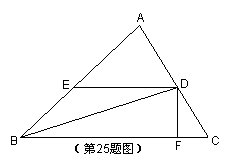25、如图，在△ABC中，AC＝15，BC＝18，
，D是AC上一个动点（D与A、C不重合），过D作DE∥BC，交AB于E，过D作DF⊥BC，垂足为F，连结BD，设CD＝x．
⑴用含x的代数式分别表示DF和BF；
⑵如果梯形EBFD的面积为S，求S关于x的函数关系式；
⑶如果BDE的面积为S1，那么x为何值时，S1有最大值，最大值是多少？
2006年中考数学第一次模拟试题
参考答案
一、选择题（每小题3分。共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | D | B | A | B | D | A | C | C |
二、填空题（每小题3分，共15分）
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
| （－2，2） | 50°和130° | 60 | 45° |
三、解答题（每小题6分，共24分）
16、解：解不等式组①得 x≥－1
解不等式组②得 x≤1
在数轴上表示不等式①、②的解集如右图：
∴原不等式组的解集是：－1≤x≤1
17、解：设方程另一根为x2，则x1=3
由根与系数关系得：3+x2=6 ∴x2=3
m=x1·x2＝3×3＝9
18、解：原式＝
=
当
，原式＝
19、解：⑴该班共有参赛学生：（1+3+6+4+2）÷2×6＝48（人）
⑵成绩落在第三组（即70.5～80.5）人数最多，共有6×3＝18（人）
⑶
20、解：⑴由条件得：
∴这个函数解析式为：
| X | 0 | 1 |
| Y=－2x+1 | 1 | －1 |
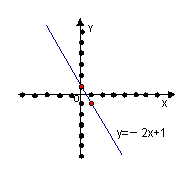⑵列表：
描点、画图如右图
|
|
22、解：根据题意可设二次函数为：
∵图象经过（－1，4）、（0，）两点
∴
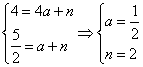
∴这个二次函数为：
24、解：⑴如图所示
在D1D上取中点M，
连结AM和MC1，即得所
走的另一条路径(A→M
→C1)
⑵设昆虫乙至少需要t秒
时间才能捕捉到昆虫甲
由勾股定理得
整理得
解这个方程得
答：昆虫乙至少需要10秒时间才能捕捉到昆虫甲。
25、解：⑴∵DF⊥BC，simC=
∴
由勾股定理得
∴
⑵∵DE∥BC
∴△AED∽△ABC
∴
∴
∴
即
⑶∵
即
∵
∴S1有最大值，当