一元二次方程与解直角三角形的检测试题
班级________姓名___________座号________________ 成绩____________
一、填空题(3分×13)
1、关于x的方程（k-√3）x²―13x + 6 = 0是一元二次方程，则k ______;
2、关于x的方程x²+ 2x ＝0的根__________________;
3、已知关于x的方程x² + mx ＋1＝0的一个根是2－√3，则方程的另一根是______;
4、若关于x的方程9x²- (k + 6)x + k + 1＝0有两个相等的实数根，则k＝______；
5、已知方程x² + mx + n＝0的两个根分别为2和－1，则m＝_______；
6、以2和-3为根的一元二次方程是____________________；
7、在RtABC中,∠C＝90º，则tanA .tanB＝___________；
8、化简1-sin²A- cos²A＝_______________；
9、在RtΔABC中，若2sin A- √2 ＋（2cosB -√3）²＝_______________；
10、 菱形中较长的对角线与较短的对角线的比为√3：1，那么菱形的锐角为____________；
11、 一个等腰三角形两边分别长为3cm和6cm，则底角的余弦值为______________；
12、 在RtΔABC 中，∠C＝Rt∠,若a＝10，SΔABC= ,则∠A＝___________；
13、 等腰梯形的底角为60º，两底边长分别为2cm和16cm，则梯形的面积为____________；
二、 选择题(4分×6)
1、如果一元二次方程2x(mx-4)＝x²-6有两个实数根，则m的最大整数值是（ ）
（A）1 （B）2 (C) 3 (D)1
2、用换元法解分式方程3(x² +2 )－7(x +2 )＋2＝0，若设 x² +2 ＝y，则换元后的方程为（ ）
(A)3y²-7y + 8＝0 （B）3y²-7y＋6＝0 （C）3y²-7y＋14＝0 （D）3y²-7y＋2＝0
3、ΔABC中，∠C＝90º，BC＝10，AB＝5√2，则B的度数为（ ）
（A）30º （B）45º （C）60º (D) 120º
3、从山顶A望地面C、D两点，它们的俯角分别是45º和30º，如果测得CD为100米，那么山高AB等于（ ）
(A) 100米 （B） 100米 （C）302米 （D）50(3 + 1)米
4、一个三角形的两边长分别为3cm和12cm，夹角为30º和它面积相等的等腰直角三角形的斜边的长为 （ ）
（A）5cm (B)6cm (C)7cm (D)8cm
5、如图，在矩形ABCD中，DE⊥AC于E，设∠ADE=
，且
,
AB
= 4, 则AD的长为（ ）．
（A）3 （B）
（C）
（D）
6、某市在“旧城改造”中计划内一
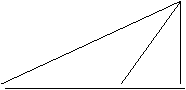
块如图所示的三角形空地上种植某种草皮以美
化环境，已知这种草皮每平方米a元，则购买这种草皮至少要（ ）．
（A）450a元 （B）225a元 （C）150a元 （D）300a元
三.解方程（6分‘×2=12）
=3
四、不解方程
，求作一个一元二次方程，使它的根比原方程各根的2倍大1.(10分)
五、甲、乙两人分别从A、B两地同时出发，匀速相向而行，在距离B地6千米外相遇，相遇后两人继续按原方向速度前进，当他们分别到达B地，A地后，又立刻返回，又在相距A地4千米外相遇，求A、B两地相距多少千米？(12分)
六、已知一船以每小时20海里的速度向正南行驶，上午10点在A外见灯塔P正东，1小时后行至B外，观察灯塔P在方位是北偏东60º，求正午12时船行驶至C外距灯塔P的距离（保留一位小数）(12分)
A P
B
七、已知，水坝横断面为梯形，坝顶宽3米，坝高4米，迎水坡，背水
坡坡度为
1：3和1：1，求水坝横断面面积；(12分)
九、在河岸一侧A外测得一建筑物CB顶端B的仰角为30º，由A向建筑物
走200米到达河边D处，测得B点的仰角为60º，求①建筑物BC地高。
②河宽DC。(12分) B
A B
30º 60º
C E A D C
D F （九）
（八）