初三数学综合训练题（一）
一、填空题（本题共6个小题）
1．点P(a, b)是直线
与双曲线
的一个交点,则以a, b两数为根的一元二次方程是（ ）
A.
B.
C.
D.
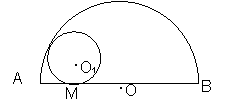
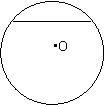
2．如图，半圆O的直径AB=4，与半圆O内切的动圆O1与AB切于点M，设⊙O 1的半径为y，AM=x，则y关于x的函数关系式是（ ）
 |
A．
B．
C．
D．
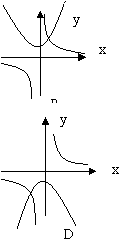
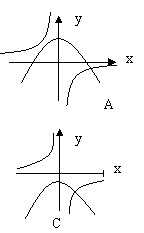
3．函数y=ax2-a与y=
(a≠0 )在同一坐标系中的图象可能是（ ）
 | |||
 | |||
4．用列表法画二次函数 的图象时先列一个表,当表中对自变量 x的值以相等间隔的值增加时,函数y 所对应的值依次为:20,56,110,182,274,380,506,650,其中有一个值不正确,这个不正确的值是（ ）
(A)506 (B)380 (C)274 (D)182
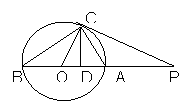
5．如图，点P是⊙O的直径BA延长线上一点，PC与⊙O相切与点C，CD⊥AB，垂足为D，连结AC、BC、OC，那么下列结论中正确结论的个数为（ ）
（1） PC2=PA.PB（2）PC.OC=OP.CD（3）OA2=OD.OP（4）OA（CP-CD）AP.CD
 | |||
 | |||
A．1 B．2 C．3 D．4
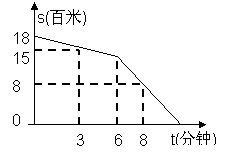
6．“高高兴兴上学来，开开心心回家去”，小明某天放学后，17时从学校出发，回家途中离家的路程s（百米）与所走的时间t（分钟）之间的函数关系如上图所示，那么这天小明到家的时间为（ ）
A．17时15分 B．17时14分 C．17时12分 D．17时11分
二、填空题（本题共8个小题，）
7．反比例函数y=
的图象经过点（tan45°,cos60°）,则k= .
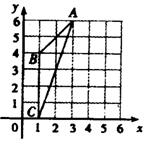
8．图中△ABC外接圆的圆心坐标是________.
9．一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5，则k的值为
.
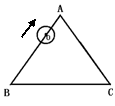
10．如图⊙O的半径为1，圆心O在正三角形的边AB上沿图示方向移动， 当⊙O移动到与AC边相切时，OA的长为 。
11．在二次函数y=ax2+bx+c(a≠0 )中，已知b是a、c的比例中项，
且当x=0时y=-4，那么y的最值为 (指明是最大值还是最小值)
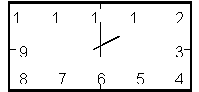12．如图为长方形时钟钟面示意图，时钟的中心在长方形对角线的交点上，长方形的宽为20cm，中面数字2在长方形的
顶点处，则长方形的长为 。
13．学校食堂出售两种厚度一样但大小不同的面饼,
小饼直径
,售价30分;大饼直径
,
售价40分.你更愿意买 饼,原因是 .
14．如果记y=
,并且
f(1)表示当x=1时y的值，即
；
表示当
时y的值，即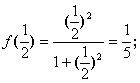
……
那么
.（结果用含n的代数式表示，n是正整数）.
四、解答题（本题共5个题，）
15．同学们对公园的滑梯很熟悉吧！如图6是某公园（六•一）前新增设的一台滑梯，该滑梯高度AC＝2m，滑梯着地点B与梯架之间的距离BC＝4m。
（1）求滑梯AB的长（精确到0.1m）；
（2）若规定滑梯的倾斜角（∠ABC）不超过45°属于安全范围。请通过计算说明这架滑梯的倾斜角是否要求？
16．已知一元二次方程x2-4x+k=0有两个不相等的实数根
(1) 求k的取值范围;
(2) 如果k是符合条件的最大整数，且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根，求此时m的值.
 |
|
|
17．已知⊙O的半径为12cm，弦AB=16cm,
(1)求圆心到弦AB的距离；
(2)如果弦AB的两个端点在圆周上滑动，那么弦的中点形成什么样的图形？
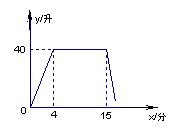
18．某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、
清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示：
根据图象解答下列问题：
（1） 洗衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？
（2） 已知洗衣机的排水速度为每分钟19升，
① 求排水时y与x之间的关系式。②如果排水时间为2分钟，求排水结束时洗
②
衣机中剩下的水量。
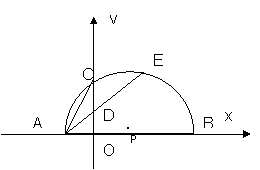
19．如图，已知两点A（-1，0）、B（4，0）在x轴上，以AB为直径的半圆P交y轴于点C.
（1）求经过A、B、C三点的抛物线的解析式；
（2）设AC的垂直平分线交OC于D，连结AD并延长AD交半圆P于点E，弧AC与弧CE相等吗？请证明你的结论.
（3）设点M为x轴的负半轴上一点，
，是否存在过点M的直线，使该直线与（1）中所得的抛物线的两个交点到y轴的距离相等？若存在，求出这条直线对应函数的解析式；若不存在，请说明理由。
初三数学综合训练题（一）参考答案
一、选择题：1.A 2.B 3.A 4.C 5.D 6.C
二、填空题：
7.
8.（5,2） 9.±
10.
11.最大值为-3 12.20
13.大；原因是：大饼合算。若答：小饼也可；（只要理由合理）14.n-;
三、解答题：
15.（1）约为4.5m （2）利用正切值比较可知：倾斜角合乎要求；
16.（1）由题意知△=16-4k>0，∴k<4
（2）由（1）知k的最大整数值为3，这时原方程为x2-x+3=0,解得：x1=1,x2=-3;
把x1=1代入x2+mx-1=0得m=0, 把x1=-3代入x2+mx-1=0得m=
;
∴m=0或
17.（1）圆心到弦AB的距离为
；
（2）以o为圆心，
cm为半径的圆。
18. （1）4分钟，40升 （2）y=-19x+325 , 2升
19.（1）
；
（2）相等；
（3）不存在。