解直角三角形
1、三角函数的定义是解直角三角形的基础,它是通过直角三角形中的两边的比导出的,锐角三角函数![]() 、
、![]() 、
、![]() 、
、![]() 都是自变量
都是自变量![]() 的函数,它们都表示一个比值。
的函数,它们都表示一个比值。
在![]() 中:
中:
![]() 的正弦
的正弦![]() ,
,![]() 的余弦
的余弦![]() ,
,![]() 的正切
的正切![]() ,
,![]() 的余切
的余切![]() ;
;
2、互为余角的三角函数的关系
![]() ;
;![]() ;
;![]() ;
;![]()
3、使用计算器求三角函数值或求角度
锐角的三角函数值可以通过使用计算器求得,反过来,由锐角的三角函数值可以求得这个角的度数。
4、特殊角的三角函数值
| 角度 |
|
|
|
| 三角函数 | 三角函数值 | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5、解直角三角形
直角三角形除了直角外,还有五个基本元素(两条直角边和斜边、两个锐角),如果知道了其中两个元素(其中至少有一条边),那么就可以求出它的另外三个元素,由直角三角形的已知元素求出它的未知元素,叫做解直角三角形。
解直角三角形主要关系式为:
①两锐角间的关系:![]()
②三边之间的关系:![]() ;
;
③边、角间的关系:![]() ;
;![]() ;
;![]() ;
;![]()
例1、求![]() 的值。(结果保留根式)
的值。(结果保留根式)
例2、已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;
;![]() 。
。
练习:1、在![]() 中,
中,![]() ,则
,则![]() 是
是![]() 的__________。
的__________。
2、把![]() 写成
写成![]() 的三角函数是____________。
的三角函数是____________。
3、在锐角![]() 中,如果
中,如果![]() ,那么
,那么![]() 的度数是___________。
的度数是___________。
4、求值:![]() ________________。
________________。
5、![]() _________________。
_________________。
6、求值:![]() 。
。
7、求适合下列各式的直角三角形的内角![]() :
:
(1)![]() ,则
,则![]() 。
。
(2)![]() ,则
,则![]() ____________。
____________。
(3)![]() ,则
,则![]() ______________。
______________。
8、在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 。
。
9、在![]() 中,若
中,若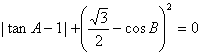 ,则
,则![]() 的大小是( )
的大小是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的大小是( )
的大小是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、在![]() 中,
中,![]() 为斜边
为斜边![]() 上的高,若
上的高,若![]() ,
,![]() ,
,![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、某水库大坝的横断面是梯形![]() ,已知坡面
,已知坡面![]() 的坡度
的坡度![]() ,坝顶宽
,坝顶宽![]() 米,斜坡
米,斜坡![]() 长
长![]() 米,坝高
米,坝高![]() 米,求:(1)坝底宽
米,求:(1)坝底宽![]() 和斜坡长
和斜坡长![]() (精确到
(精确到![]() 米);(2)坡角
米);(2)坡角![]()
13、根据下列条件解三角形
(1)![]() ,
,![]() ,
,![]() ,求
,求![]() 、
、![]() 、
、![]() 及三角形面积;
及三角形面积;
(2)![]() ,
,![]() ,三角形面积为
,三角形面积为![]() ,求
,求![]() 、
、![]() 、
、![]() 及
及![]()