初三数学竞赛试题
班 姓名
一、选择题
1.一条抛物线![]() 的顶点为
的顶点为![]() ,
,![]() ,且与x轴的两个交点的横坐标为一正一负,则a、b、c中为正数的( ).
,且与x轴的两个交点的横坐标为一正一负,则a、b、c中为正数的( ).
(A)只有![]() (B)只有
(B)只有![]() (C)只有
(C)只有![]() (D)只有
(D)只有![]() 和
和![]()
|
 往返跑训练.已知:甲上山的速度是a米
往返跑训练.已知:甲上山的速度是a米
|
上山的速度是![]() a米/分,下山的速度是
a米/分,下山的速度是
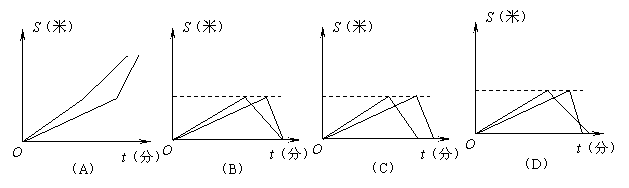
2b米/分.如果甲、乙二人同时从点A出发,时间为t(分),离开点A的路程为S(米).那么下面图象中,大致表示甲、乙二人从点A出发后的时间t(分)与离开点A的路程S(米)之间的函数关系的是( )
3.已知方程![]()
![]() 的两根之比为1∶2,判别式的值为1,则p,q的值分别是
( )
的两根之比为1∶2,判别式的值为1,则p,q的值分别是
( )
(A) p=1,q= 2
(B) p=3,q= 2
(C) p=![]() 3,q= 2 (D) p=3,q=
3,q= 2 (D) p=3,q=![]() 2
2
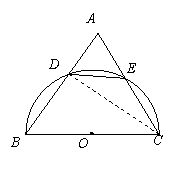 4.如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,
4.如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,
AC与D,E两点,且cosA=![]() ,则S△ADE∶S四边形DBCE的值为
( )
,则S△ADE∶S四边形DBCE的值为
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
 5.如图所示,在△ABC中,DE∥AB∥FG,且FG到DE、AB的
5.如图所示,在△ABC中,DE∥AB∥FG,且FG到DE、AB的
距离之比为1:2. 若△ABC的面积为32,△CDE的面积为2,
则△CFG的面积S等于 ( ).
(A)6 (B)8
| |
6.如果x和y是非零实数,使得![]() 和
和![]() ,7.请用计算器计算下列各式,
,7.请用计算器计算下列各式,
(A)3 (B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题
7.请用计算器计算下列各式,
3×4,33×34,333×334,3333×3334.
根据各式中的规律,直接写出333333×333334的结果是 .
8.如果将字母a,b,c,d,e按“aababcabcdabcdeaababcabcdabcde…”这样的方式进行排列,那么第2004个字母应该是 .
9.已知,![]() (
(![]() >0),则
>0),则![]() .
.
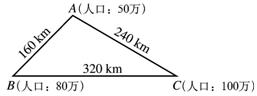
10.据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数m、n(单位:万人)以及两城市间的距离d(单位:km)有![]() 的关系(k为常数) . 现测得A、B、C三个城市的人口及它们之间的距离如图所示,且已知A、B两个城市间每天的电话通话次数为t,那么B、C两个城市间每天的电话通话次数为
次(用t表示).
的关系(k为常数) . 现测得A、B、C三个城市的人口及它们之间的距离如图所示,且已知A、B两个城市间每天的电话通话次数为t,那么B、C两个城市间每天的电话通话次数为
次(用t表示).

11.已知:如图,在△ABC中,BC边的长为12,且这边上的高AD的长为3,则△ABC的周长的最小值为 .
12.实数x、y、z满足x+y+z=5,xy+yz+zx=3,则z的最大值是 .
三、解答题(共3题,每小题20分,满分60分)
13.一列客车始终作匀速运动,它通过长为450米的桥时,从车头上桥到车尾下桥共用33秒;它穿过长760米的隧道时,整个车身都在隧道里的时间为22秒. 从客车的对面开来一列长度为a米,速度为每秒v米的货车,两车交错,从车头相遇到车尾相离共用t秒.
(1)写出用a、v表示t的函数解析式;
(2)若货车的速度不低于每秒12米,且不到每秒15米,其长度为324米,求两车交错所用时间的取值范围.
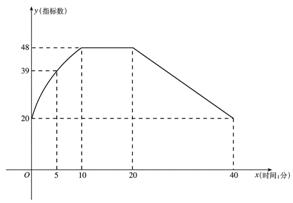
14.通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散. 学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中). 当![]() 时,图象是抛物线的一部分,当
时,图象是抛物线的一部分,当![]() 和
和![]() 时,图象是线段.
时,图象是线段.
(1)当![]() 时,求注意力指标数y与时间x的函数关系式;
时,求注意力指标数y与时间x的函数关系式;
(2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
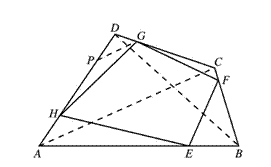 15.设点E、F、G、H分别在面积为1的四边形ABCD的边AB、BC、CD、DA上,且
15.设点E、F、G、H分别在面积为1的四边形ABCD的边AB、BC、CD、DA上,且![]() (k是正数),求四边形EFGH的面积.
(k是正数),求四边形EFGH的面积.
参考答案:
一、选择题
1.(A)2、(C).3、(C).4、(A).5、(B)6、(D)
二、填空题
7. 333333×333334=.8、c. 9. ![]() 10.
10. ![]() 11. 12+
11. 12+![]() 12.
12. ![]()
三、解答题(共3题,每小题20分,满分60分)
13.
解:(1)设客车的速度为每秒x米,客车的长度为y米. 依题意知
![]() 解出
解出![]()
所以,![]() .
.
(2)当![]() ,
,![]() 时,
时,
由(1)得![]() .
.
又因为![]() ,所以,
,所以,![]() .
.
故t的取值范围为![]() .
.
14. 解:(1)当![]() 时,设抛物线的函数关系式为
时,设抛物线的函数关系式为![]() ,由于它的图象经过点(0,20),(5,39),(10,48),所以
,由于它的图象经过点(0,20),(5,39),(10,48),所以
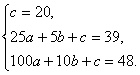
解得,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
(2)当![]() 时,
时,![]() .
.
所以,当![]() 时,令y=36,得
时,令y=36,得![]() ,
,
解得x=4,![]() (舍去);
(舍去);
当![]() 时,令 y=36,得
时,令 y=36,得![]() ,解得
,解得
![]() .
.
因为![]() ,所以,老师可以经过适当的安排,在学生注意力指标数不低于36时,讲授完这道竞赛题.
,所以,老师可以经过适当的安排,在学生注意力指标数不低于36时,讲授完这道竞赛题.
 15.解:连结AC,过点G作GP∥AC交DH于点P,有
15.解:连结AC,过点G作GP∥AC交DH于点P,有
![]() .
.
由已知![]() ,则
,则![]() .
.
于是有![]() ,从而
,从而![]() .
.
又由于△DPG∽△DAC,我们有![]() ,故
,故![]() .
.
因此![]() .
①
.
①
同理 ![]() .
②
.
②
①+②得![]() .
.
连结BD,同理可证![]() .所以
.所以
![]() .
.
答:四边形EFGH的面积是![]() .
.