2004--2005学年度河西区第二学期九年级第二次质量调查
数学试题
第I卷（选择题 共30分）
一. 选择题：本大题共10小题，每小题3分，共30分。在每小题给出四个选项中，只有
一项是符合题目要求的。
1. 实数
，
，
中，分数的个数是（
）
A. 0 B. 1 C. 2 D. 3
2. 已知
为锐角，且
，则的度数是（
）
A. 30° B. 45° C. 60° D. 90°
3. 已知
，则代数式
的值为（
）
A. 
B. 
C. 
D. 
4. 已知
，且
，则
的值为（
）
A. 2 B. 
C. 
D. 0
5. 下列形状的地砖中，不能把地面作既无缝隙又不重叠覆盖的地砖是（ ）
A. 正三角形 B. 正方形 C. 正五边形 D. 长方形
6. 如图，两圆轮叠放在墙边，若两圆的半径分别为R和
，则它们与墙的切点A、B间的距离为（）
A. 
B. 
C. 
D. 
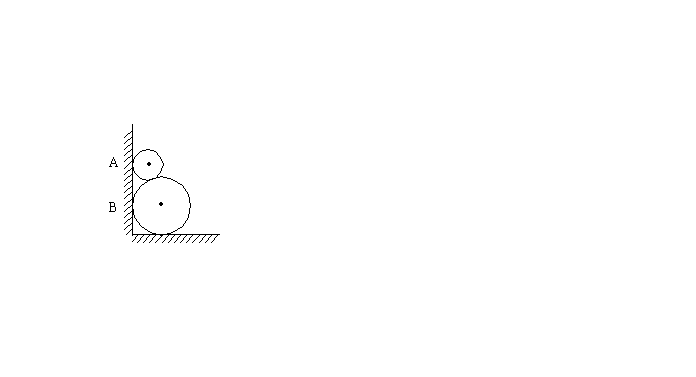
7. 已知抛物线
的对称轴为
，且经过点（3，0），则
的值（
）
A. 等于0 B. 等于1 C. 等于D. 不能确定
8. 如图所示，E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是（）
A. 
B. 
C. 
D. 
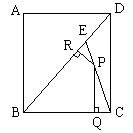
9. 下面给出四个命题：
① 各边相等的六边形是正六边形；
② 顶角和底边对应相等的两个等腰三角形全等；
③ 顺次连结一个四边形各边中点所成的四边形是矩形，则原四边形是菱形；
④ 正五边形既是中心对称图形又是轴对称图形
其中真命题有（ ）
A. 0个 B. 1个 C. 2个 D. 4个
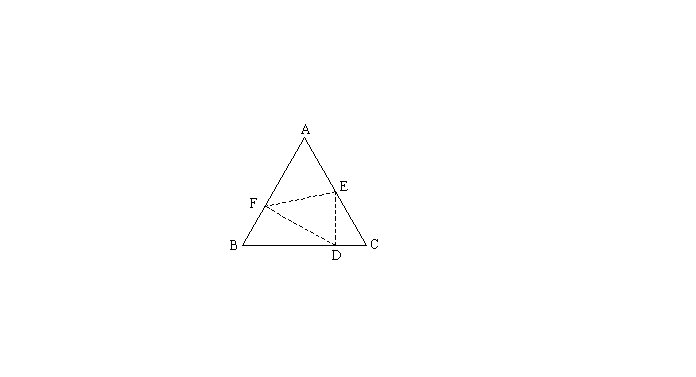
10. 如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置，且ED⊥BC，则CE的长是（）
A. 
B. 
C. 
D. 
第II卷（非选择题 共90分）
二. 填空题：本大题共8小题，每小题3分，共24分。请将答案直接填在题中横线上。
11. 不等式组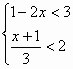
的解集是
。
12. 若非零实数a、b满足
，则
= 。
13. 一次函数
中，函数y随x的增大而减小，且其图象不经过第一象限，则m的取值范围是 。
14. 已知某一铁路桥长1000米，现有一列火车从桥上通过，测得火车从开始上桥到完全过桥共用1分钟，整个火车完全在桥上的时间为40秒，则火车的速度是 。
15. 已知一个梯形的面积为10cm2，高为2cm，则该梯形的中位线的长等于 cm。
16. 如图，
是等边三角形，⊙O与AC边相切于A点，与BC边交于E点，与AB的延长线交于D点，已知BE=6，CE=4，则BD的长为 。
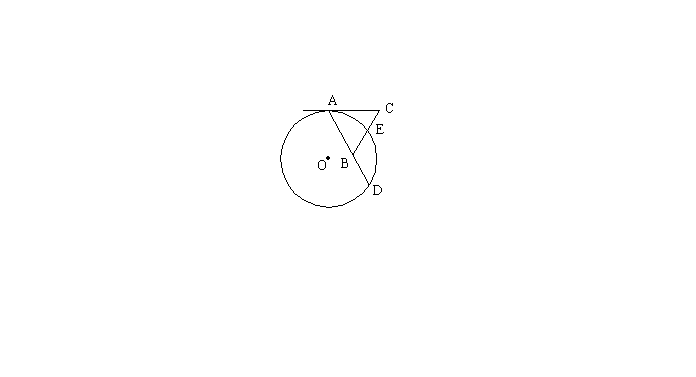
17. 如图，内接于⊙O，D是劣弧
上一点，AE交⊙O于F，为使
应补充的一个条件是
或 。
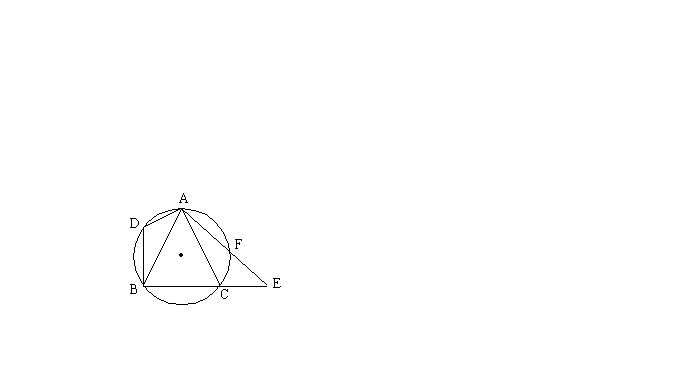
18. 在矩形ABCD的边AB上找一点，使点E与C、D的连线将矩形分成三个彼此相似的三角形，这样的E点存在的个数是 。
三. 解答题：本大题共8小题，共66分。解答应写出文字说明、演算步骤或证明过程。
19.（本小题6分）
某班40名学生的某次数学测验成绩统计表如下：
| 成绩（分） | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数（人） | 2 | x | 10 | y | 4 | 2 |
（1）若这个班的数学平均成绩是69分，求x和y的值；
（2）此班40名学生成绩的众数、中位数分别是多少？
20.（本小题8分）
解方程：
21.（本小题8分）
已知：二次函数
（1）求证：该函数的图象一定与x轴有两个不同的交点；
（2）设该函数的图象与x轴的交点坐标为（
）、（
），且
，求m的值，并求出该函数图象的顶点坐标。
22.（本小题8分）
如图，反比例函数
的图象经过点
，过A作AB⊥x轴于点B，
的面积为
。
（1）求k和m的值；
（2）若过A点的直线
与x轴交于C点，且
，求此直线的解析式。
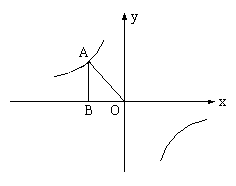
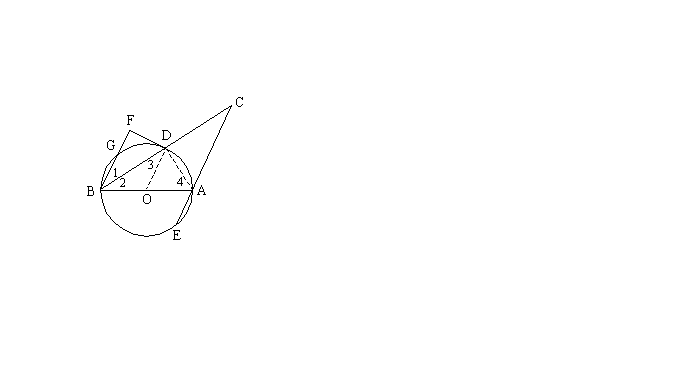
23.（本小题8分）
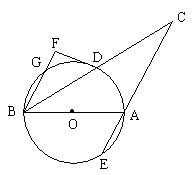
如图，AB是⊙O的直径，DF切⊙O于点D，BF⊥DF于F，过点A作AC∥BF交BD的延长线于点C。
（1）求证：
；
（2）设CA的延长线交⊙O于E，BF交⊙O于G，若
的度数等于
，试简要说明点D和点E关于直线AB对称的理由。
24.（本小题8分）
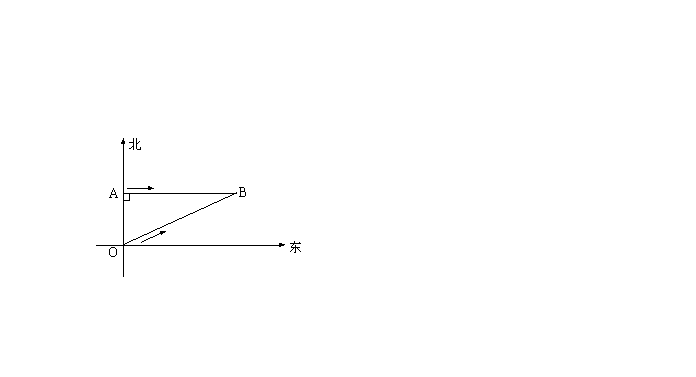
民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只，正以24海里/小时的速度向正东方向航行。为迅速实施检查，巡逻艇调整好航向，以26海里/小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问（1）需要几小时才能追上？（点B为追上时的位置）（2）确定巡逻艇的追赶方向（精确到
）。
参考数据：
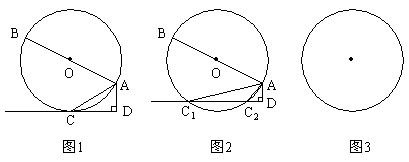
25.（本小题10分）
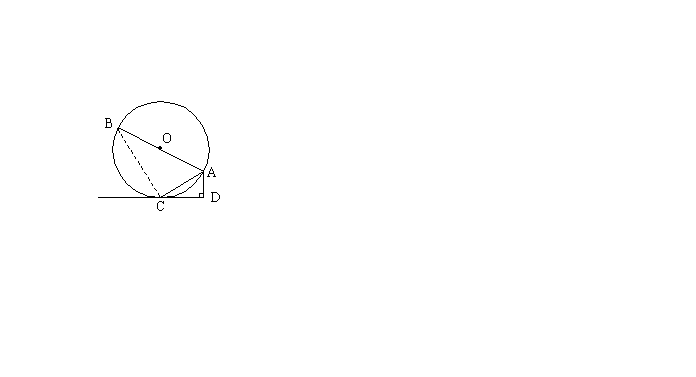
如图1，AB是⊙O的直径，AC是弦，直线CD切⊙O于点C，AD⊥CD，垂足为D。
（1）求证：
（2）若将直线CD向上平移，交⊙O于C1、C2两点，其他条件不变，可得到图2所示的图形，试探索AC1、AC2、AB、AD之间的关系，并说明理由；
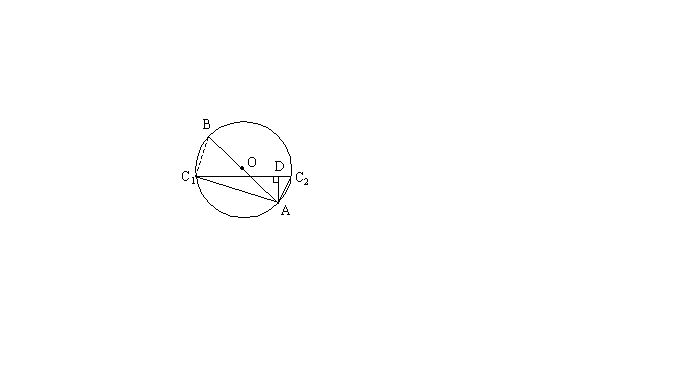
（3）把直线C1D继续向上平移，使弦C1C2与直径AB相交（交点不与A、B重合），其他条件不变。请你在图3中画出变化后的图形，标好相应字母。并试着写出与（2）相应的结论，判断你的结论是否成立？若不成立，请说明理由；若成立，请给出证明。
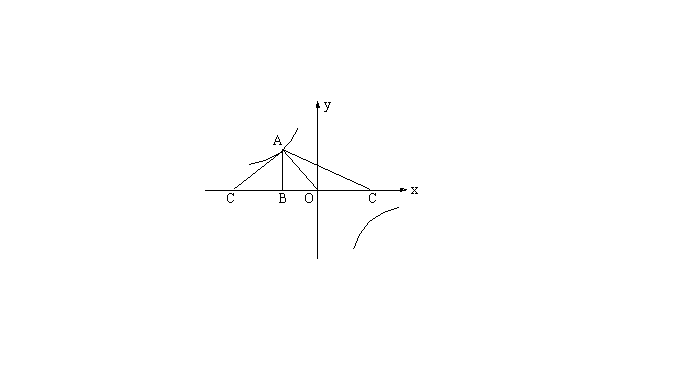
26.（本小题10分）
已知抛物线与x轴相交于两点A（）和B（）（
），与y轴相交于点C，坐标原点O到A、B、C三点的距离OA、OB、OC满足
，直线
与双曲线
均过抛物线的顶点，试确定抛物线的解析式。
2004�2005学年度河西区第二学期九年级第二次质量调查
数学试题参考答案及评分标准
一. 选择题：（本大题共10小题，每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | B | B | C | D | A | A | B | D |
二. 填空题：（本大题共8小题，每小题3分，共24分）
11. 
12. 2
13. 
14. 20米/秒
15. 5
16. 9
17. 
18. 当
时，符合题意的点E存在两个；当AB=2AD时，符合题意的点E存在一个；当
时，符合题意的点E不存在。
三. 解答题：
19. 解：
（1）由题意得
（2分）
解得
（4分）
（2）这班学生的成绩的众数是60，中位数是65。（6分）
20. 解：原方程可化为
。（1分）
设
，则
解得
，
（3分）
当时，
，即
∴
（5分）
当时，
，即
此方程无解（7分）
经检验：是原方程的根（8分）
21.
（1）证明：
∴一元二次方程
有两个不相等的实数根，因而函数的图象一定与x轴有两个不同的交点。（2分）
（2）
该函数的图象与x轴的两个交点坐标分别为
∴
、
是方程的两个实数根
∴
，
，由（4分）
∴得，
，因此
（6分）
∴二次函数的解析式为
，因此坐标顶点为（2，
）（8分）
22. 解：
（1）
在第二象限，
∴
，
，∴ 
（2分）
∴ 
将A（
，2）代入
中得，
（4分）
注：方法不唯一，只要求（2分）求出（2分）
（2）由（1）知，
，∵
∴
（6分）
∴ C（
，0）或（，0），可得直线解析式为：
，或
（8分）
23.
（1）证法一：连结OD，∵ FD是⊙O的切线 ∴ OD⊥FD（1分）
∵ BF⊥FD，∴ OD∥BF，∴ ∠1=∠3（2分）
∵ OB=OD，∴ 
（3分）
∵ AC∥BF，∴
（4分）
∴ 
，即（5分）
证法二：连结AD，∵ FD是⊙O的切线，∴ 
（2分）
∵ 
是⊙O的直径，∴ 
，∴
（4分）
∵ AC∥BF，∴
，∴
，即（5分）
（2）∵ 的度数为
，∴
，
∴ 
的度数为，
，
（6分）
∴ 
的度数，∴
（7分）
∵ AB是直径，∴ D点和E点关于直线AB对称（8分）
24. 解：设需要t小时才能追上，则：AB=24t，OB=26t
（1）在
即：（
）2=
（2分）
解得：
不合题意，舍去。
∴ 
即：需要1小时才能追上（4分）
（2）在
，∵
（6分）
∴ 
即：巡逻艇的追赶方向为北偏东
（8分）
25.
（1）证明：连接BC，∵ AB是⊙O的直径，∴ 
∵ 
，∴
∴
（1分）
又 ∵ CD切⊙O于C，∴ 
∴
（2分）
∴ 
∴
（3分）
（2）关系：
（4分）
理由是：连接BC1，∵ 四边形ABC1C2是圆内接四边形
∴ 
（5分）
同（1）有
∴
∴ 
∴
（6分）
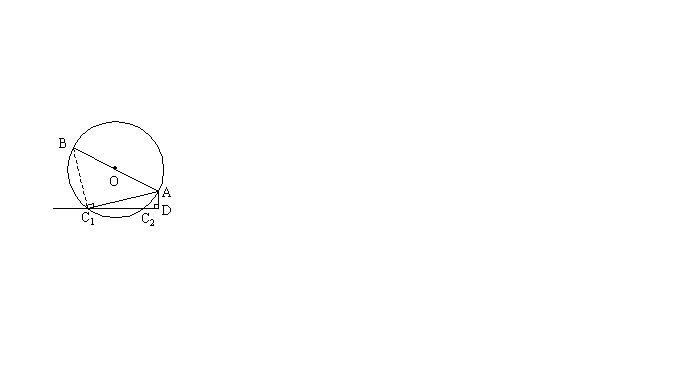
（3）画图。（7分）
结论是：（8分）
证明：连接
同（1）有又
∵ 
∴ ∴
∴
（10分）
26. 解：由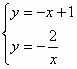
，解得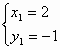
；
、
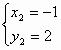（1）若抛物线以（2，）为顶点，则抛物线开口必须向上，对称轴为，
如图2、图1所示，所以有
，
故
，与矛盾，
即抛物线不可能以（2，）为顶点。（3分）
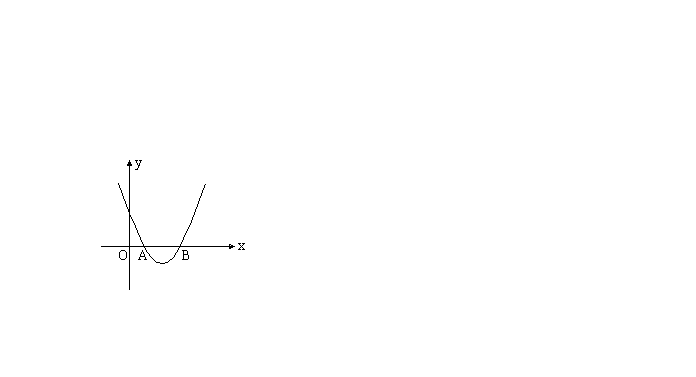
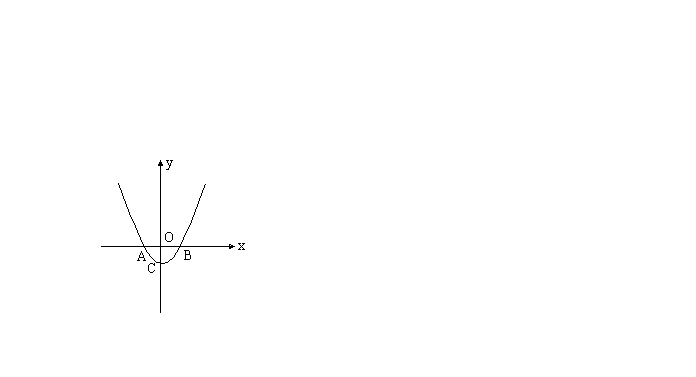
（2）若抛物线以（，2）为顶点，则抛物线开口必须向下，
且
和
，可得
，
∴ 抛物线为
（5分）
① 若A、B都在原点的左侧，则C点必在
轴负半轴上，
可得
，
，
∴ 由，得
∴ 
，即
∴ 
，解得
此时
，故不合题意，舍去（8分）
② 若点B在原点右侧，则C点必在轴正半轴上，由于A一定在
轴负半轴上，
∴ 
，
，
由
，即
∴ 
，
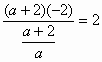∴ 所求的解析式为
（10分）