和平区2004--2005学年度第二学期九年级数学模拟试卷
第I卷(选择题 共30分)
一. 选择题:(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 下列运算中,正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2. 已知![]() 和
和![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() 的值是(
)
的值是(
)
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
3. 已知二次函数的图象如图所示,那么此函数的解析式只可能是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
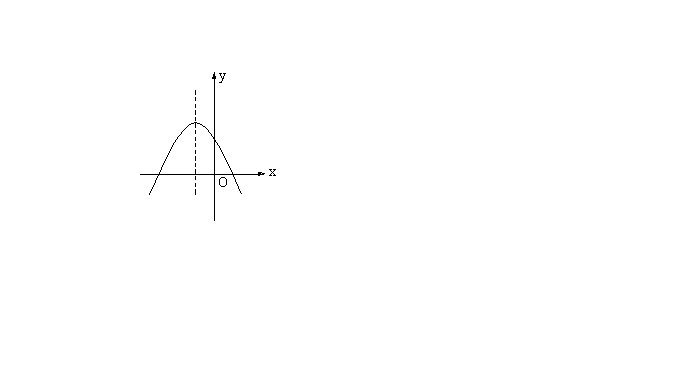
4. 若顺次连结四边形各边的中点,得到一个菱形,则这个四边形( )
A. 是矩形 B. 是等腰梯形
C. 是平行四边形 D. 两条对角线相等
5. 甲、乙、丙、丁四支足球队在世界杯预选赛中进球数分别为:9,9,x,7,若这组数据的众数与平均数恰好相等,则这组数据的中位数是()
A. 10 B. 9 C. 8 D. 7
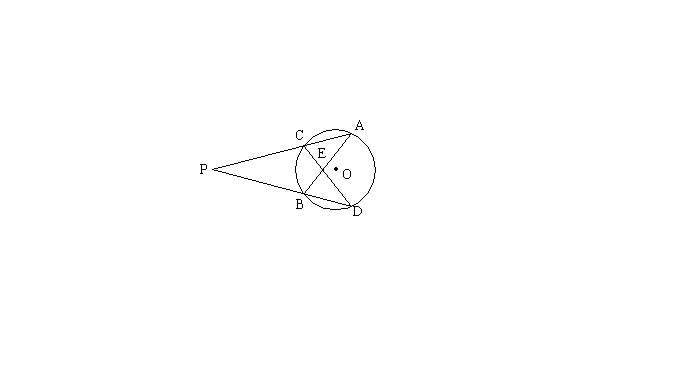
6. 如图,⊙O的两条弦AB、CD相交于点E,AC和DB的延长线交于点P,下列结论中成立的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
7. 有如下四个结论:
① 既是轴对称图形,又是中心对称图形的四边形是菱形;
② 一个多边形的所有内角中,最多只有3个是锐角;
③ 正五边形的每一个内角都等于108°;
④ 两圆的公切线最少有1条,最多有4条。
其中正确结论的个数为()
A. 1个 B. 2个 C. 3个 D. 4个
8. 如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点![]() ,已知AB=1cm,则爬行路线最短为()
,已知AB=1cm,则爬行路线最短为()
A. 3cm B. ![]() C.
C. ![]() D.
D. ![]()
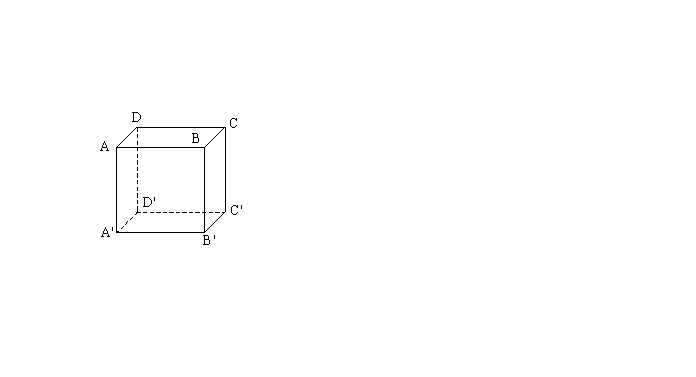
9. 如图,![]() 是等边三角形,点D、E分别为边BC、AC上的点,且CD=AE,点F是BE和AD的交点,BG⊥AD于G点,已知
是等边三角形,点D、E分别为边BC、AC上的点,且CD=AE,点F是BE和AD的交点,BG⊥AD于G点,已知![]() ,FG=1,则AB的长为( )
,FG=1,则AB的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
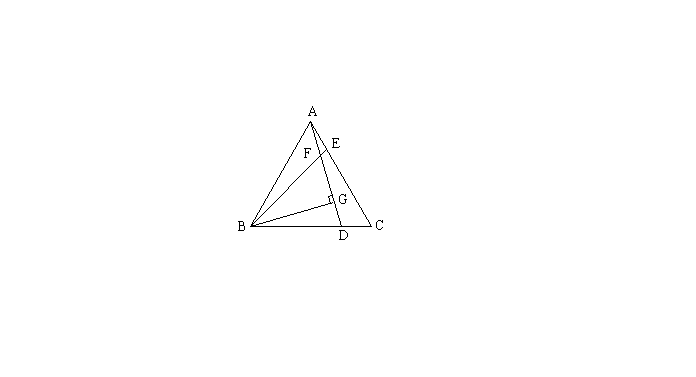
10. 实数![]() 、
、![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 的值为(
)
的值为(
)
A. 2 B. 3 C. 4 D. 5
第II卷(非选择题 共90分)
二. 填空题:(本大题共8小题,每小题3分,共24分,请将答案直接填在题中横线上。)
11. 若![]() ,则锐角
,则锐角![]() 。
。
12. 已知![]() ,则
,则![]() 。
。
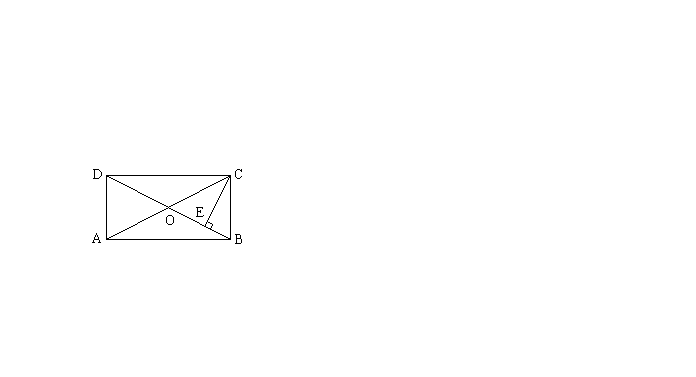
13. 如图,矩形ABCD中CE⊥BD于E,若![]() ,则
,则![]() 度。
度。
14. 若![]() 、
、![]() 都是有限小数,
都是有限小数,![]() ,且
,且![]() ,则
,则![]() 、
、![]() 的值可以是
。(填上一组满足条件的值即可)
的值可以是
。(填上一组满足条件的值即可)
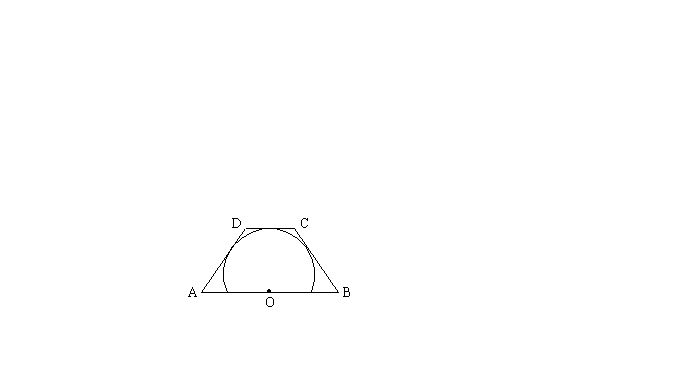
15. 如图,O点在梯形ABCD的下底AB上,且⊙O与梯形的上底及两腰都相切,若AB=5cm,CD=2cm,则梯形ABCD的周长等于 。
16. 一条直线过点(1,0),且该直线与抛物线![]() 只有一个交点,则这个交点的坐标为
。
只有一个交点,则这个交点的坐标为
。
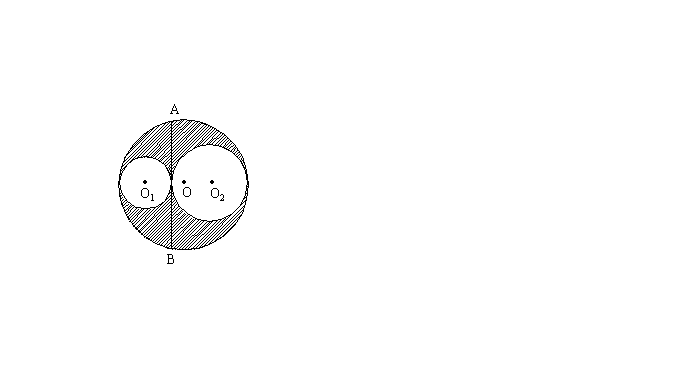
17. 如图,⊙O1与⊙O2相外切,且都与⊙O相内切,⊙O1与⊙O2的内公切线交⊙O于A、B两点,若AB=4cm,则阴影部分的面积为 cm2。
18. 已知抛物线![]() 与
与![]() 轴交于A(
轴交于A(![]() ,
,![]() ),B(
),B(![]() ,0)两点,且
,0)两点,且![]() ,则
,则![]() 。
。
三. 解答题:(本大题共8小题,共66分,解答应写出文字说明、演算步骤或证明过程。)
19.(本题6分)
计算:![]()
20.(本题8分)
解方程组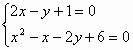
21.(本小题8分)
已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点(
的图象交于点(![]() ,2),求:(1)这两个函数的解析式;(2)两个函数图象另一个交点的坐标。
,2),求:(1)这两个函数的解析式;(2)两个函数图象另一个交点的坐标。
22.(本小题8分)
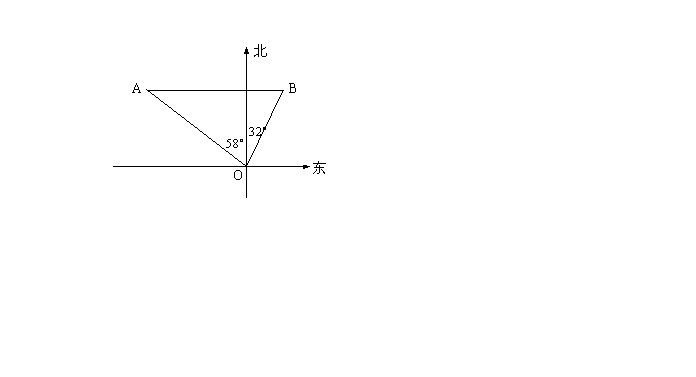
如图,甲、乙两船同时从港口O出发,甲船以16.1海里/时的速度向北偏西58°方向航行,乙船向北偏东32°方向航行,航行了两个小时,甲船到达A处并观测到B处的乙船恰好在其正东方向,求乙船的速度![]() (精确到0.1海里/时)。
(精确到0.1海里/时)。
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
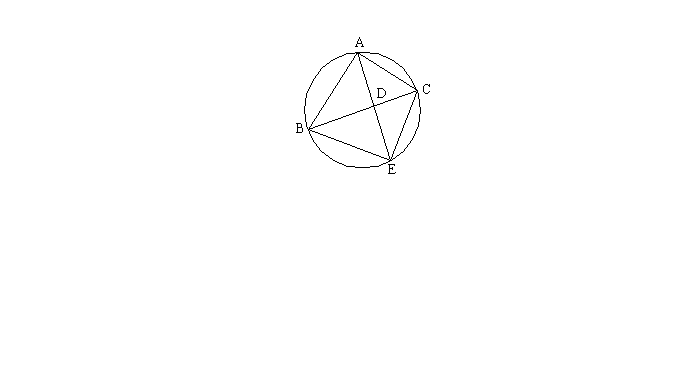
23.(本小题8分)
如图,E是![]() 外接圆上一点,AE交BC于D点,且
外接圆上一点,AE交BC于D点,且![]() 。
。
(1)求证:BE=CE;
(2)若AB=8cm,AC=6cm,BC=10cm,求BE的长。
24.(本小题8分)
甲乙两车从相距360千米的两地相向而行,如果乙车比甲车早出发1.5小时,那么两车恰好在路途中点相遇;如果同时出发,那么5小时后,两车相距90千米,求两车的速度。
25.(本小题10分)
已知:如图,AB是⊙O的直径,AC切⊙O于A点,且AC=AB,CO交⊙O于P、D两点,BP的延长线交AC于E点。
(1)求证:DA∥BE;
(2)求证:![]() ;
;
(3)求![]() 的值。
的值。
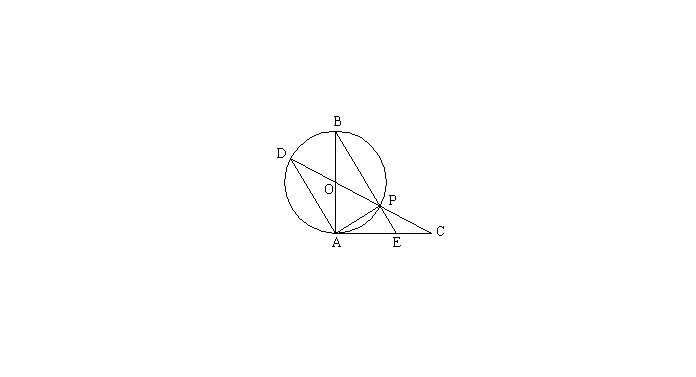
26.(本小题10分)
已知抛物线![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 中
中![]() 、
、![]() 、
、![]() 的对边。
的对边。
(1)求证:该抛物线与![]() 轴必有两个交点;
轴必有两个交点;
(2)设抛物线与![]() 轴的两个交点为P、Q,顶点为R,
轴的两个交点为P、Q,顶点为R,![]() ,已知
,已知![]() ,
,![]() 的周长为10,求抛物线的解析式;
的周长为10,求抛物线的解析式;
(3)设直线![]() 与抛物线交于点E、F,与
与抛物线交于点E、F,与![]() 轴交于点M,抛物线与
轴交于点M,抛物线与![]() 轴交于点N,若抛物线的对称轴为
轴交于点N,若抛物线的对称轴为![]() ,
,![]() 与
与![]() 的面积之比为
的面积之比为![]() ,试判断三角形的形状,并证明你的结论。
,试判断三角形的形状,并证明你的结论。
和平区2004�2005学年度第二学期九年级数学模拟试卷参考答案及评分标准
一. 选择题(本大题共10小题,每小题3分,共30分)
1. B 2. A 3. C 4. D 5. B 6. D 7. B 8. C 9. A 10. C
二. 填空题(本大题共8小题,每小题3分,共24分)
11. 50°
12. ![]() 13. 45
13. 45
14. 0.4和2.5(或为:0.5和2,![]() 和
和![]() ,……等)
,……等)
15. 12cm
16.(0,0)或(1,1)或(2,4)
17. ![]()
18. ![]()
三. 解答题(本大题共8小题,共66分)
19.(本小题6分)
解:原式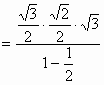 (3分)
(3分)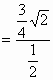 (5分)
(5分)![]() (6分)
(6分)
20.(本小题8分)
解: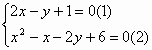
由(1),得![]() (3)(1分)
(3)(1分)
把(3)代入(2),整理,得![]() (2分)
(2分)
解这个方程,得![]() ,
,![]() (4分)
(4分)
把![]() 代入(3),得
代入(3),得![]() 3
3
把![]() 代入(3),得
代入(3),得![]() (6分)
(6分)
所以原方程组的解是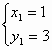 ,
,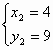 (8分)
(8分)
21.(本小题8分)
解:
(1)根据题意,得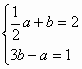 (2分)
(2分)
解这个方程组,得![]() (3分) ∴ 一次函数的解析式为:
(3分) ∴ 一次函数的解析式为:![]()
反比例函数的解析式为:![]() (5分)
(5分)
(2)由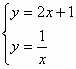 解得
解得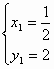 ,
,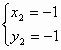 (7分)
(7分)
∴ 这两个函数图象另一个交点的坐标为(![]() ,
,![]() )(8分)
)(8分)
22.(本小题8分)
解:根据题意,得OA=![]() (海里)(1分)
(海里)(1分)
![]() (2分)
(2分)
∵ B在A的正东方向
∴ ![]() (3分)
(3分)
在![]() 中,
中,![]() (5分)
(5分)
∴ ![]()
![]() (海里)(7分)
(海里)(7分)
∴ ![]() (海里/时)(8分)
(海里/时)(8分)
答:乙船的速度约为10.1海里/时。
23.(本小题8分)
(1)证明:在![]() 和
和![]() 中,∵
中,∵
![]() ,
,![]()
∴ ![]() (2分) ∴
(2分) ∴ ![]()
∵ ![]() ∴
∴
![]() (3分)
(3分)
∴ BE=CE(4分)
(2)解:∵ AB=8cm,AC=6cm,BC=10cm
∴ ![]() ,
,![]()
∴ ![]() (5分)
(5分)
∴ ![]() 是直角三角形,且
是直角三角形,且![]() (6分)
(6分)
∴ BC为圆的直径,![]() (6分)
(6分)
由(1)可知,在![]() 中,BE=CE
中,BE=CE
∴ ![]() (7分)
(7分)
∴ ![]() (8分)
(8分)
24.(本小题8分)
解:设甲车的速度为![]() 千米/时,乙车的速度为
千米/时,乙车的速度为![]() 千米/时(1分)
千米/时(1分)
根据题意,得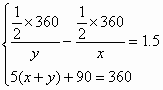 (3分)
(3分)
解这个方程组,得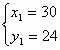 ,
,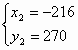 (4分)
(4分)
经检验,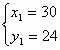 ,
,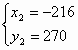 都是分式方程组的解(5分)
都是分式方程组的解(5分)
而![]() (不合题意,舍去)(6分) ∴
(不合题意,舍去)(6分) ∴ ![]() (7分)
(7分)
答:甲车的速度为30千米/时,乙车的速度为24千米/时(8分)
25.(本小题10分)
(1)证明:
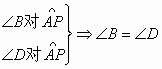
![]() (1分)
(1分)
![]() (2分)
(2分)![]() (3分)
(3分)
(2)证明:
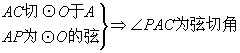
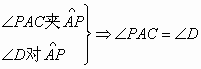 (4分)
(4分)
![]() (5分)
(5分)
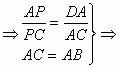
![]() (6分)
(6分)
(3)解:设![]() ,(
,(![]() ),⊙O的直径为
),⊙O的直径为![]()
则DP=AB=AC=![]()
由切割线定理,得![]() (7分)
(7分)
即![]() ,整理,得
,整理,得![]()
解得![]()
∴ ![]() ,
,![]() (8分)
(8分)
∵ BE∥DA ∴
![]()
即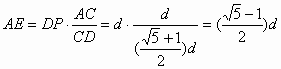 (9分)
(9分)
∵ ![]()
∴ 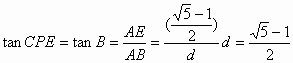 (10分)
(10分)
26.(本小题10分)
(1)证明:在关于![]() 的一元二次方程
的一元二次方程![]() 中,
中,
![]() (1分)
(1分)
∵ ![]() 、
、![]() 、
、![]() 是
是![]() 的边长,∴
的边长,∴
![]() ,
,![]() (2分)
(2分)
∴ ![]() ,方程有两个不相等的实数根
,方程有两个不相等的实数根
∴ 抛物线![]() 与
与![]() 轴必有两个交点(3分)
轴必有两个交点(3分)
(2)解:由![]() ,得
,得![]() (4分)
(4分)
设抛物线的对称轴交![]() 轴于H,如图, 则
轴于H,如图, 则![]()
![]() 由
由![]()
得![]() (6分)
(6分)
解得![]() ,则
,则![]()
∴ 抛物线的解析式为:![]() (7分)
(7分)
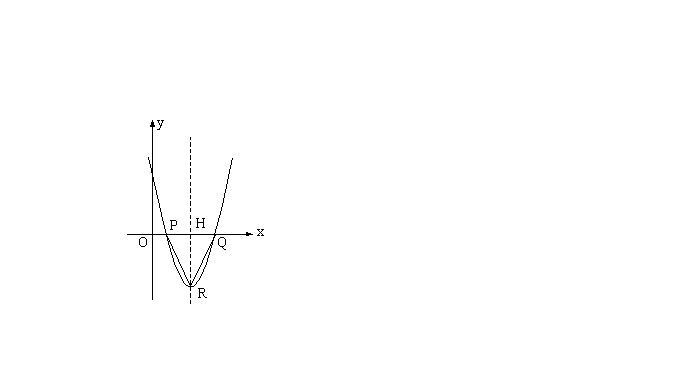
(3)解:由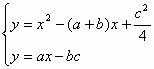
得![]()
由题意,得![]() ∴
∴
![]()
则![]() (8分)
(8分)
如图,设E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() )
)
由![]() ,得
,得![]()
∴ 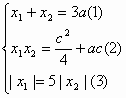
由(3)得![]() 或
或![]()
由(2)得![]()
∴ ![]() (9分)
(9分)
由(1)得![]() ,即
,即![]()
∵ ![]() ∴
∴
![]()
∴ ![]() ∴
∴
![]() ∴
∴
![]() 为等边三角形(10分)
为等边三角形(10分)