二十八中数学竟赛第二次选拔赛试题
(人教版初三年级时间120分钟满分150分)
一. 选择题(每小题5分,共50分)以下每题的四个结论中,仅有一个是正确的,请将表示正确答案的英文字母填在每题后面的圆括号内。
1. 化简代数式![]() 的结果是( )
的结果是( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
2. 已知多项式![]() 除以
除以![]() 时,所得的余数是1,除以
时,所得的余数是1,除以![]() 时所得的余数是3,那么多项式
时所得的余数是3,那么多项式![]() 除以
除以![]() 时,所得的余式是( )
时,所得的余式是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 已知![]() 且
且![]() ,那么( )
,那么( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则
![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5. 若一个三角形的一个外角的平分线平行于三角形的一条边,则此三角形肯定是( )
A. 直角三角形 B. 等边三角形
C. 等腰三角形 D. 等腰直角三角形
6. 若![]() 的三边长是a、b、c,且满足
的三边长是a、b、c,且满足![]() ,
,![]() ,
,![]() ,则
,则![]() 是( )
是( )
A. 钝角三角形 B. 直角三角形
C. 等腰直角三角形 D. 等边三角形
7. 平面内有n条直线(![]() ),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则
),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
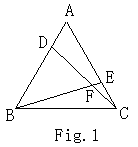
8. In fig. 1, let ![]() be an equilateral
triangle, D and E be points on edges AB and AC respectively, F be intersection
of segments BE and CD, and
be an equilateral
triangle, D and E be points on edges AB and AC respectively, F be intersection
of segments BE and CD, and ![]() , then the magnitude relation between Ad and CE is ( )
, then the magnitude relation between Ad and CE is ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
indefinite
D.
indefinite
(英汉词典:equilateral等边的;intersection交点;magnitude大小,量;indefinite不确定的)
9. 已知两个不同的质数p,q满足下列关系:
![]() ,m是适当的整数,那么
,m是适当的整数,那么![]() 的数值是( )
的数值是( )
A. B. C. D.
10. 小张上周工作a小时,每小时的工资为b元,本周他的工作时间比上周减少10%,而每小时的工资数额增加10%,则他本周的工资总额与上周的工资总额相比( )
A. 增加1% B. 减少1% C. 增加1.5% D. 减少1.5%
二. 填空题(每小题6分,共60分)
11. 化简:![]() 的结果是_________。
的结果是_________。
12. 已知p、q为实数,且![]() ,满足
,满足![]() ,那么
,那么![]() 的值等于_______。
的值等于_______。
13. 无理数![]() 的整数部分是________。
的整数部分是________。
14. 设a、b、c均为不小于3的实数,则![]() 的最小值是_____。
的最小值是_____。
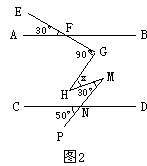
15. 如图2,直线![]() ,
,
![]() ,则
,则![]() 的大小是_____。
的大小是_____。
16. 代数式![]() 的最小值是_______。
的最小值是_______。
17. 有大小两个杯子,大杯中盛满48升纯酒精,第一次倒出一小杯纯酒精后,用水加满大杯,第二次又倒出一小杯混合溶液,再用水加满大杯,这时大杯中还剩余27升纯酒精,那么小杯的容积是________。
18. If ![]() and
and ![]() are unequal
primes,
are unequal
primes, ![]() and
and ![]() are unequal positive integers satisfying
are unequal positive integers satisfying ![]() and
and ![]() , then the value of
, then the value of ![]() is ________。
is ________。
(英汉词典:prime质数)
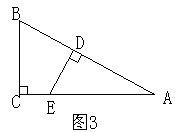
19. 如图3,![]() 中,
中,![]() ,点D、E分别在AB、AC上,且
,点D、E分别在AB、AC上,且![]() ,若DE将
,若DE将![]() 分成面积相等的两部分,那么线段CE与AE的长度的比是________。
分成面积相等的两部分,那么线段CE与AE的长度的比是________。
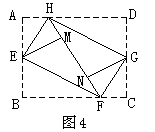
20. 如图4,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若![]() ,那么线段AD与AB的比等于_________。
,那么线段AD与AB的比等于_________。
三. 解答题(21、22题各13分,23题14分,共40分)要求:写出推算过程
21. 六个排球队参加小组循环赛,取前4名参加第二阶段比赛,每赛一场,胜队得一分,负队不得分,且没有平局,结果有3个队并列第一名,一个队得第四名,他们得到了小组出线权,请写出各队得分的情况,并说明理由。
22. 从甲站到乙站共有800千米,开始400千米是平路,接着300千米是上坡路,余下的是下坡路,已知火车在上坡路、平路、下坡路上的速度的比是3:4:5,
(1)若火车在平路上的速度是80千米/小时,那么它从甲站到乙站所用的时间比从乙站到甲站所用的时间多多少小时?
(2)若要求火车来回所用的时间相同,那么火车从甲站到乙站在平路上的速度与乙站到甲站在平路上的速度的比是多少?
23. 如图5,等边![]() 的边长
的边长![]() ,点P是
,点P是![]() 内的一点,且
内的一点,且
![]() ,若
,若![]() ,求PA、PB的长。
,求PA、PB的长。
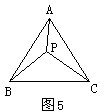
〖答案〗
一. 选择题(本大题共50分。对于每个小题,答对,得5分;答错或不答,不给分)
1. D 2. A 3. B 4. A 5. C
6. D 7. D 8. C 9. B 10. B
二. 填空题:
11. ![]() 12.
0 13. 33 14.
12.
0 13. 33 14. ![]()
15. ![]() 16.
13 17. 12升 18. 5
16.
13 17. 12升 18. 5
19. ![]() 20.
20. ![]()
三. 解答题:
21. 设各队得分分别是![]() ,
,
且![]()
因为六个队之间共比赛![]() 场,
场,
所以![]()
首先,最后两名之间也有一场比赛,所以![]() 不可能都得0,
不可能都得0,
因而![]() ,
,![]() ,
,
即![]()
当![]() 时,
时,![]()
所以![]()
当![]() 时,
时,![]() ,
,
则![]() 可以被3整除,
可以被3整除,
因此![]() ,
,
所以![]()
因为![]() ,所以
,所以![]() ,
,
此时![]() 与
与![]() 矛盾,
矛盾,
所以当![]() 时无解,
时无解,
因此6个队得分分别是4,4,4,2,1,0。
22. (1)甲乙两地之间的距离是800千米,开始400千米是平路,接着300千米是上坡路,所以下坡路是100千米,火车在平路上的速度是800千米/小时,所以火车在上坡路上的速度是600千米/小时,在下坡路上的速度是100千米/小时,所以
从甲地到乙地用的时间为
![]() 小时,
小时,
从乙地到甲地用的时间为
![]() 小时,
小时,
所以从甲地到乙地用的时间比从乙地到甲地用的时间多![]() 小时。
小时。
(2)设火车从甲地到乙地在平路上的速度是![]() 千米/小时,则它在上坡路上的速度是
千米/小时,则它在上坡路上的速度是![]() 千米/小时,在下坡路上的速度是
千米/小时,在下坡路上的速度是![]() 千米/小时,
千米/小时,
所以火车从甲地到乙地用的时间是
![]() 小时
小时
同样,设火车从乙地到甲地在平路上的速度是![]() 千米/小时,则它在上坡路上的速度是
千米/小时,则它在上坡路上的速度是![]() 千米/小时,在下坡路上的速度是
千米/小时,在下坡路上的速度是![]() 千米/小时,所以火车从乙地到甲地用的时间是
千米/小时,所以火车从乙地到甲地用的时间是
![]() 小时
小时
依题意有![]() ,
,
所以![]()
23. 设![]() 的面积分别是
的面积分别是![]() ,线段PA、PB、PC的长分别是x、y、z,如图,
,线段PA、PB、PC的长分别是x、y、z,如图,
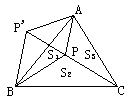
把![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() ,得
,得![]() ,连接
,连接![]() ,则
,则![]() 是等边三角形且边长
是等边三角形且边长![]() ,因为
,因为
![]() ,
,
即![]() ,
,
及![]() ,
,
所以在![]() 中,满足
中,满足![]()
则![]() 是直角三角形
是直角三角形
于是![]() ,
,
即![]()
将![]() 绕B顺时针旋转
绕B顺时针旋转![]() ,将
,将![]() 绕C逆时针转
绕C逆时针转![]() ,可分别得
,可分别得
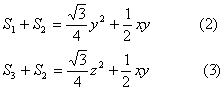
![]() 得
得
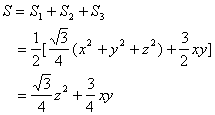
又![]() ,所以
,所以![]() ,
,
即![]()
又由已知和(4)得
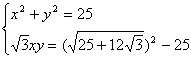
所以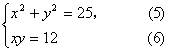
因为![]() ,
,
解方程得![]()
所以![]()