番禺区2006年九年级数学综合训练(一)
本试卷分选择题和非选择题两部分,共三大题25小题,满分150分.考试时间为120分钟.
注意事项:
1.答卷前,考生务必在答题卡第1页上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名;填写考场试室号、座位号,再用2B铅笔把对应这两个号码的标号涂黑.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B铅笔画图.答案必须写在答题卡各题目指定区域内的相应位置上;如需要改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域.不准使用铅笔、圆珠笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回.
第一部分 选择题(共30分)
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
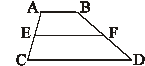 1.如图所示,在梯形
1.如图所示,在梯形![]() 中,
中,![]() E、F分别是线段
E、F分别是线段![]() 和
和![]() 的中点,且
的中点,且![]() ,那么线段
,那么线段![]() 的长是( ※ ).
的长是( ※ ).
![]() (A)1.5 (B)2 (C)2.5 (D)4
(A)1.5 (B)2 (C)2.5 (D)4
2.下列事件中,是必然事件的是(※)
(A)打开电视机,正在播放广告 (B)父亲的年龄比儿子年龄大
(C)广州冬天不下雨 (D)下雨时,每个人都会打着伞避雨
3.据广东省气象台“天气预报”报道,2006年3月15日广州市的最低气温是11℃,最高
气温是18℃,则广州市的当天气温![]() (℃)的范围是(※)
(℃)的范围是(※)
(A)![]() <11 (B)
<11 (B)![]() >18 (C)
>18 (C)![]() (D)11≤
(D)11≤![]() ≤18
≤18
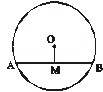
4.如图,⊙![]() 的直径为 6,圆心
的直径为 6,圆心![]() 到弦
到弦![]() 的距离
的距离![]() 的长为1, 则弦AB的长是(※)
的长为1, 则弦AB的长是(※)
 (A)5
(B)
(A)5
(B)![]()
(C)![]() (D)
(D)![]()
![]()
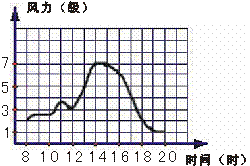 5.春天来了,暖湿气流送来了和暖的南风. 红星中学
5.春天来了,暖湿气流送来了和暖的南风. 红星中学
某课外活动小组观测了今年4月2日连续12个小时的
风力变化情况,并画出了风力随时间变化的图象(如
右图). 根据此图,下列说法中正确的一个是(※)
(A)8时风力最小,14时风力最大;
(B)在8时至12时,风力最大为7级;
![]() (C)在8时至14时,风力总是在不断增大;
(C)在8时至14时,风力总是在不断增大;
(D)在15时至20时,风力不断减小;20时风力最小.
6.在下列五个图形中,图①表示的是由一个长方体和一个圆锥组合在一起的模块,在②③④⑤这四个图形中,是这个模块的俯视图的是(※)
(A) ② (B) ③ (C)④ (D) ⑤

① ② ③ ④ ⑤
7. 王皓同学用计算器计算发现![]()
![]()
![]() 据此他总结出了一条规律:“
据此他总结出了一条规律:“![]() ”,并高兴地告诉了同桌刘英,刘英看后告诉他这个命题是假命题,不成立,并举了一个反例予以说明.刘英同学举出的反例可以是(※)
”,并高兴地告诉了同桌刘英,刘英看后告诉他这个命题是假命题,不成立,并举了一个反例予以说明.刘英同学举出的反例可以是(※)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
8. 已知![]() 、
、![]() 是⊙
是⊙![]() 的两条直径,则四边形
的两条直径,则四边形![]() 一定是(※)
一定是(※)
(A)菱形 (B)矩形 (C)正方形 (D)等腰梯形
9.关于x的方程![]() 有实数根,则
有实数根,则![]() 的取值范围是(※)
的取值范围是(※)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10. 在下列分别标有①、②、③、④序号的图形中,每个图形的缺口都能与标有序号⑤的图形缺口相吻合,则能与标有序号⑤的图形拼成一个梯形的图形上所标识的序号是(※)
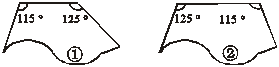 (A) ① (B)②
(A) ① (B)②
(C) ③ (D)④
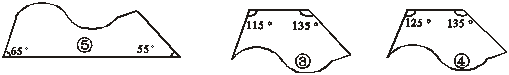
![]()
第二部分 非选择题(共120分)
 二、填空题(本大题共6小题,每小题3分,满分18分.)
二、填空题(本大题共6小题,每小题3分,满分18分.)
![]() 11.已知一个圆形细菌的直径长约为0.000015米,那么这个细菌的直径长用科学记数法可表示为 ※ 米。
11.已知一个圆形细菌的直径长约为0.000015米,那么这个细菌的直径长用科学记数法可表示为 ※ 米。
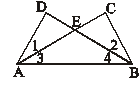
12. 如图,给出下列论断:①![]() , ②
, ②![]() ,
,
③![]() ,请你将其中的两个作为条件,另一个作为结 论,构成一个真命题:
※
※ ※
;
,请你将其中的两个作为条件,另一个作为结 论,构成一个真命题:
※
※ ※
;
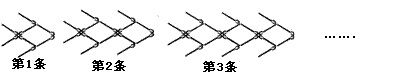
13. 如下图是小明用火柴搭的第1条、第2条、第3条“金鱼”……,则他搭第8条“金鱼”时需要火柴棒 ※ 根.
 |
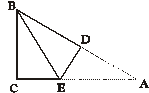
14. 在三角形纸片![]() 中,
中,![]() ,
,![]()
![]() .折叠该纸片,使点
.折叠该纸片,使点![]() 与
与![]() 重合,折痕与
重合,折痕与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() (如图),则折痕
(如图),则折痕![]() 的长为 ※ .
的长为 ※ .
![]()
![]()
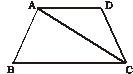
15. 如图,在梯形![]() 中,
中,![]() ,如果要使
,如果要使![]() ∽
∽![]() ,那么还需要补充的一个条件是 ※ .(只要求写出一个条件即可,不必考虑所有可能情况)
,那么还需要补充的一个条件是 ※ .(只要求写出一个条件即可,不必考虑所有可能情况)
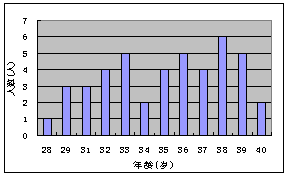 16.四年一度的费尔兹奖是国际数学界的最
16.四年一度的费尔兹奖是国际数学界的最
高奖之一,主要是颁赠给年轻的、已做
出一定成就的数学家.右图所示的条形
图是截至2004年底止的44位费尔兹奖
得主获奖时的年龄统计图,通过统计图
可知费尔兹奖得主获奖时年龄的众数是
※ 岁,平均年龄是 ※ 岁,
获奖时年龄不超过33岁(含33岁)的
青年数学家共有 ※ 位.
三、解答题(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分9分)
解方程:![]() .
.
18.(本小题满分9分)
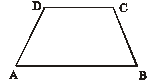 如图,在等腰梯形ABCD中,
如图,在等腰梯形ABCD中,![]() ,
,![]() ,
,
(1)用直尺和圆规作出线段![]() 的垂直平分线
的垂直平分线![]() ,并标出
,并标出
直线![]() 与线段
与线段![]() 的交点
的交点![]() (不必写作法,但要保
(不必写作法,但要保
![]() 留作图痕迹).
留作图痕迹).
(2)连结![]() 、
、![]() ,证明:△ADM≌△BCM.
,证明:△ADM≌△BCM.
19. (本小题满分10分,每小题5分)
(1) 分解因式:![]() ;
;
(2)若代数式![]() 的值为
的值为![]() ,试求实数
,试求实数![]() 的值.
的值.
20.(本小题满分10分)
李小明同学每天骑自行车上学,途中必须经过三个安装有红绿灯的十字路口,每个路口红灯和绿灯每分钟依次各亮30秒.
(1)小明是个遵守交通规则的好学生.每周一他值日,希望能尽快赶到学校,他说“要是上学途中一路上都遇到绿灯就好了”.他这一愿望有可能实现吗?
(2)小明上学途中只遇到一次红灯的概率大,还是恰好遇到两次红灯的概率大?为什么?请用树状图加以分析.
21.(本小题满分12分)如图,直线![]() 分别与x轴、y轴相交于A、B两点,O为坐标原点,A点的坐标为(4,0).
分别与x轴、y轴相交于A、B两点,O为坐标原点,A点的坐标为(4,0).
(1)求k的值;
(2)若P为线段![]() (
(![]() 、B点除外)上的一点,过P作
、B点除外)上的一点,过P作![]() ⊥
⊥![]() 轴,
轴,![]() ⊥
⊥![]() 轴,垂足分别为
轴,垂足分别为![]() 、
、![]() ,得矩形
,得矩形![]() ,设线段
,设线段![]() 的长为
的长为![]() ,矩形的面积为
,矩形的面积为![]() ,当点P在线段
,当点P在线段![]() (A、B两端点除外)上移动时,求
(A、B两端点除外)上移动时,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)求当![]() 取何值时,面积S取最大值,并求出这个最大值.
取何值时,面积S取最大值,并求出这个最大值.
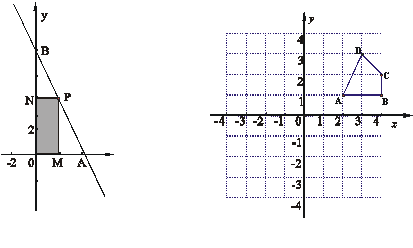
![]()
![]()
22.(本小题满分12分)
在如图所示的平面直角坐标系中,有一个四边形![]() .
.
(1)作四边形![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() (不写作法),写出
(不写作法),写出![]() 点的坐标;
点的坐标;
(2)以原点![]() 为旋转中心,将四边形
为旋转中心,将四边形![]() 顺时针旋转
顺时针旋转![]() 得到四边形
得到四边形![]() ,
,
试画出图形(不写作法),并观察四边形![]() 与四边形
与四边形![]() 有何对称关系?
有何对称关系?
(3)又连结![]() 、
、![]() ,判断
,判断![]() 与
与![]() 是否垂直,并说明理由.
是否垂直,并说明理由.
23.(本小题满分12分)
番禺德兴大桥是一座下承式混凝土连续拱圈梁组合桥,桥面上有三对抛物线形拱圈. 如图是其中一个拱圈的实物照片,据有关资料记载此拱圈高![]() 为10.0米(含拱圈厚度和拉杆长度),横向分跨
为10.0米(含拱圈厚度和拉杆长度),横向分跨![]() 为40.0米.
为40.0米.
(1)试在图中建立适当的直角坐标系,求出拱圈外沿抛物线的解析式;
(2)在桥面![]() (
(![]() 的中点)处装有一盏路灯,为了保障安全规定路灯距拱圈的距离
的中点)处装有一盏路灯,为了保障安全规定路灯距拱圈的距离![]() 不得少于1.1米,试求路灯支柱
不得少于1.1米,试求路灯支柱![]() 的最低高度(结果精确到0.1米)
的最低高度(结果精确到0.1米)

![]()
|
24.(本小题满分14分)
清河市场一位水果销售商到某果园去批发荔枝和芒果,为了方便运输和冷藏保鲜,果园用统一规格的竹筐装荔枝,每筐装10㎏,用硬纸箱装芒果,每箱装12㎏.
(1)该销售商第一次进货荔枝26筐, 芒果18箱,共用去4328元,已知每千克的荔枝进货价格比芒果进货价格贵25%,试求荔枝、芒果的进货价格;
(2)该销售商在售完第一批水果后发现:扣除运输费用后,销售一筐荔枝可获利15元,销售一箱芒果能获利8元,且荔枝的销量较大,约是芒果的两倍.于是该销售商根据这一市场行情再次进货(只租一辆车,这辆车完全装荔枝的话最多能装40筐,两筐荔枝的位置恰好能装3箱芒果),计划所购荔枝的筐数是芒果箱数的两倍再加3(筐),且售后所获利润不少于500元,试问怎样进货较好?为什么?
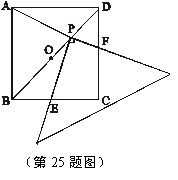
25.(本小题满分14分)
如图,![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 的对称中心,
的对称中心,![]() 为
为![]() 上一点,
上一点,![]() (
(![]() ),连结
),连结![]() ,把一个边长均大于
,把一个边长均大于![]() 的直角三角板的直角顶点放置于
的直角三角板的直角顶点放置于![]() 点处,让三角板绕
点处,让三角板绕![]() 点旋转,旋转时保持三角板的两直角边分别与正方形的
点旋转,旋转时保持三角板的两直角边分别与正方形的![]() 、
、![]() 边(含端点)相交,其交点为
边(含端点)相交,其交点为![]() 、
、![]() .
.
(1)在旋转过程中,![]() 的长能否与
的长能否与![]() 的长相等?若能,请作出此时点
的长相等?若能,请作出此时点![]() 的位置,并给出证明,若不能,请说明理由.
的位置,并给出证明,若不能,请说明理由.
(2)探究在旋转过程中,线段![]() 与
与![]() 长的大小关系,并对你得出的结论给予证明.
长的大小关系,并对你得出的结论给予证明.
(3)探究在旋转过程中,四边形![]() 的面积
的面积![]() 是否发生变化?若不变化,求出定值
是否发生变化?若不变化,求出定值![]() ;若发生变化,试求出面积
;若发生变化,试求出面积![]() 的变化范围(用含
的变化范围(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
 |
番禺区2006年九年级数学综合训练(一)
参考答案和评分标准
一、选择题(本大题共10小题,每小题3分,满分30分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | D | D | D | A | C | B | C | A |
二、填空题(共6题,每题3分,共18分.)
11.![]() ; 12.(开放题)若①②成立,则③成立等.(①②
; 12.(开放题)若①②成立,则③成立等.(①②![]() ③,①③
③,①③![]() ②,②③
②,②③![]() ①任填一种均可;)
①任填一种均可;)
13.50; 14.1;15.![]() 或
或![]() 或
或![]() ; 16.38,35,16.
; 16.38,35,16.
三、解答题(本大题共9小题,满分102分.)
17.解:![]() ,(3分)
,(3分) ![]() ,(6分) 故原方程的解是
,(6分) 故原方程的解是![]() ,或
,或![]() (9分).
(9分).
评分说明:若掉一个根扣3分.
18.(1)作图3分(图略)
(2)证明:![]() 四边形
四边形![]() 等腰梯形,
等腰梯形, ![]() ,(4分)
,(4分)
又![]() 为
为![]() 垂直平分线
垂直平分线![]() 上一点,
上一点,![]() .(6分)
.(6分)
![]()
![]() 即:
即:![]() (7分)
(7分)
而![]() ,
,![]() △ADM≌△BCM(SAS). (9分)
△ADM≌△BCM(SAS). (9分)
评分说明:其余类似的方法可比照给分,在证明全等过程中,三个条件每缺少一个扣2分.
19.解:(1)原式![]() (3分)
(3分)![]() (5分).
(5分).
(2)![]()
![]()
![]()
![]() (8分)
(8分)

![]() (9分),
(9分),![]() (10分)
(10分)
20.解:(1)可以实现(4分).
(2)小明上学途中只遇到一次红灯的概率与恰好遇到两次红灯的
概率相等(5分).作树状图如右图:(8分),观察树状图得知:
只遇到一次红灯的概率为![]() ,恰好遇到两次红灯的概率也为
,恰好遇到两次红灯的概率也为![]() ,
,
故两者概率相等(10分).
21.解:(1)由![]() 得
得![]() (3分)
(3分)
(2)由题意得![]() (5分),故
(5分),故![]() (7分,各1分)
(7分,各1分)
(3)![]() (8分)
(8分)![]() (10分)
(10分)
故当![]() 时,面积S取最大值
时,面积S取最大值![]() .(12分)
.(12分)
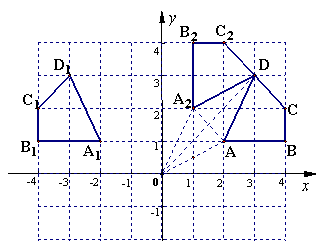 22.解:(1)如图.(4分,错一个点扣1分)
22.解:(1)如图.(4分,错一个点扣1分)
(2)如图,其中![]() 与
与![]() 重合.(8分,错一个点扣1分)
重合.(8分,错一个点扣1分)
经作图观察得知:
两个四边形关于直线![]() 对称.(9分)
对称.(9分)
(3)由点的位置及格点构造知:
![]() .
.
![]() 四边形
四边形![]() 为菱形. (11分)
为菱形. (11分)
![]() (12分)
(12分)
23.解:(1)建系方法一:如图以![]() 为坐标原点,
为坐标原点,![]() 所在
所在
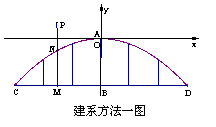 直线为
直线为![]() 轴建立如图所示直角坐标系
轴建立如图所示直角坐标系![]() ,(2分)
,(2分)
因拱圈外沿所在的抛物线过原点,且以![]() 轴为对称轴,
轴为对称轴,
故可设抛物线方程为:![]() ,(4分)
,(4分)
由题意抛物线过点![]() ,代入得
,代入得![]() ,
,
故拱圈外沿抛物线的解析式为![]() (6分)
(6分)
评分说明:其余建系方法可比照给分.如图建系方法二的方程为:![]()
建系方法三的方程为:![]()
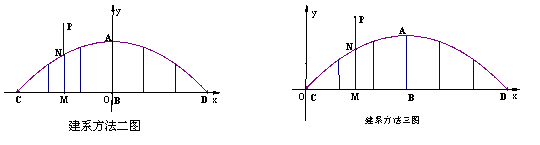 |
(2)设![]() ,(8分)则:
,(8分)则:![]() (10分)
(10分)
![]() ,(11分)
,(11分)
![]()
即路灯支柱![]() 的最低高度为
的最低高度为![]() 米.(其余解法可类似给分)(12分)
米.(其余解法可类似给分)(12分)
24.解:(1)设荔枝、芒果的进货价格分别为![]() (元/㎏)、
(元/㎏)、![]() (元/㎏), (1分)则由题意有:
(元/㎏), (1分)则由题意有:
![]() ,(5分,各2分)解之得:
,(5分,各2分)解之得:![]()
故荔枝、芒果的进货价格分别为10元/㎏、8元/㎏. (6分)
(2) 设芒果箱数为![]() 为整数),则所购荔枝的筐数是
为整数),则所购荔枝的筐数是![]() (7分),则由题意得:
(7分),则由题意得:
![]() (9分,各1分),解之得:
(9分,各1分),解之得: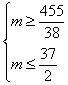 ,而
,而![]() 为整数,故有
为整数,故有![]() (11分)(1分)
(11分)(1分)
再考虑装车运载条件限制,两筐荔枝的位置恰好可装3箱芒果,分别取
![]() ……
……
列表如下: (12分)
| 芒果( | 12 | 13 | 14 | … |
| 荔枝( | 27 | 29 | 31 | … |
| 能否装车 | 能 | 能 | 否 | … |
| 能获利润 | 27×15+12×8=501(元) | 29×15+13×8=539(元) | … |
从上表可以发现![]() 时均可满足进货要求,但当
时均可满足进货要求,但当![]() 时,虽然利润进一步增加但不能满足装车要求.故要获最大利润则该销售商最佳的进货方式为:
时,虽然利润进一步增加但不能满足装车要求.故要获最大利润则该销售商最佳的进货方式为:
进29筐荔枝和13箱芒果可获得最大利润539元.(14分)
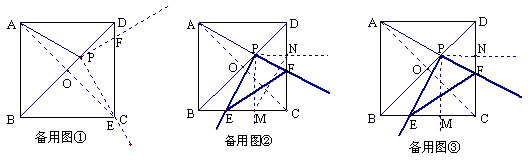
25.【解】(1)如图①当![]() 运动到
运动到![]() 位置时(点
位置时(点![]() 与
与![]() 重合)时(或者以
重合)时(或者以![]() 为圆心,以
为圆心,以![]() 为半径画弧得与
为半径画弧得与![]() 的另一个交点
的另一个交点![]() ),
),![]() =
=![]() . (1分)
. (1分)
证明:连![]() ,
,![]() 正方形
正方形![]() 是以
是以![]() 对称中心的中心对称图形,
对称中心的中心对称图形,
![]() 重直平分
重直平分![]() , (2分)
, (2分)
 又
又![]() 为
为![]() 上一点,
上一点,![]() ,即此时
,即此时![]() =
=![]() . (3分)
. (3分)
(2)探究结论:在旋转过程中,线段![]()
![]()
![]() . (5分)
. (5分)
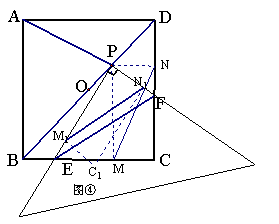
证明(方法一): 如图②,过![]() 作
作![]() 作
作![]() 垂足分别为
垂足分别为![]() ,则四边形
,则四边形![]() 为矩形,
为矩形,
![]() (6分)
(6分)
在![]() 中,
中,![]() , 在
, 在![]() 中,
中,![]() , (7分)
, (7分)
又在![]() 中,
中,![]() , 在
, 在![]() 中,
中,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (9分)
(9分)
证明(方法二):如图④同法一作矩形![]() .
.
![]() (6分)
(6分)
旋转矩形![]() 使
使![]() 、
、![]() 分别与直角板的直角边重合,
分别与直角板的直角边重合,
记此时![]() 、
、![]() 的位置分别为
的位置分别为![]() 、
、![]() ,则
,则![]()
![]() .(8分)
.(8分)
而![]() ,故点
,故点![]() 在线段
在线段![]() 上,同理点
上,同理点![]() 在线段
在线段![]() 上,且有
上,且有![]() .
.
![]()
![]()
![]() . (9分)
. (9分)
(3)探究结论:在旋转过程中,四边形![]() 的面积
的面积![]() 发生变化. (10分)
发生变化. (10分)
如图③,当点![]() 在
在![]() 上时,设
上时,设![]() ,
,![]() (
(![]() ),
),
![]() ,
,![]() ,
,
![]() ,
,![]()
![]()
![]() . (11分)
. (11分)
故当![]() 时, 面积
时, 面积![]() 取最大值
取最大值![]() . (12分)
. (12分)
同理,当点![]() 在
在![]() 上时,设
上时,设![]() ,
,
![]()
![]()
![]()
如图当点![]() 与
与![]() 重合时
重合时![]() 时, 面积
时, 面积![]() 取最小值
取最小值![]() (13分)
(13分)
![]() 面积
面积![]() 的取值范围是:
的取值范围是: ![]()
![]()
![]() .
(14分)
.
(14分)