北京市西城区抽样测试初三数学试卷
一、选择题（共12个小题，第1~4小题每题3分，第5~12小题每题4分，共44分）
在每个小题给出的四个备选答案中，只有一个是符合题目要求的。请把正确结论的代号写在题后的括号内。
1. 如果实数a满足
，且
，那么a的值为（ ）
A. 
B.
0 C. 3 D. 
2. 
可化简为（ ）
A. 
B. 
C. 
D. 
3. 菱形的周长为20cm，两条对角线的比为4:3，那么此菱形的面积等于（ ）
A. 
B. 
C. 
D. 
4. 如果两个圆只有1条公切线，那么这两个圆的位置关系为（ ）
A. 外离 B. 相交 C. 外切 D. 内切
5. 不等式
的解集在数轴上表示正确的是（
）
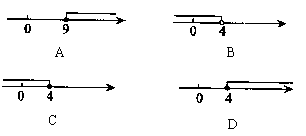
6. 如图，PA、PB分别与⊙O相切于点A、点B，
，点C在⊙O上的位置如图所示，那么
等于（
）
A. 30° B. 45° C. 60° D. 75°
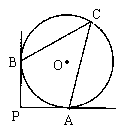
7. A、B、C三种物质的质量m（千克）与体积V（米3）的关系如图所示，那么这三种物质的密度
的大小关系为（
）
A. 
B. 
C. 
D. 
8. 如果圆锥的母线长为10cm，高为8cm，那么它的侧面积等于（ ）
A. 
B. 
C. 
D. 
9. 已知关于x的方程
的两个实数根互为倒数，那么k的值为（）
A. 1 B. 
C. 
D. 
10. 函数
的共同性质是（
）
A. 它们的图象都经过原点
B. 它们的图象都不经过第二象限
C. 在x>0的条件下，y都随x的增大而增大
D. 在x>0的条件下，y都随x的增大而减小
11. 如图，将矩形ABCD绕点C顺时针旋转，使点D落在BC边延长线上的F点，如果
，那么点A从旋转开始到结束走过的路线长度为（）
A. 
B. 
C. 
D. 
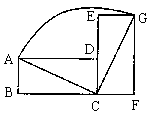
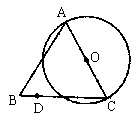
12. 如图，
是边长为10的等边三角形，以AC为直径作⊙O，D是BC边上一点，
，以D为圆心，DB为半径的⊙D与⊙O的位置关系为（）
A. 相交 B. 外离 C. 外切 D. 内切
二、填空题（共5个小题，每小题4分，共20分）
13. 函数
中，自变量x的取值范围是________
14. 如果某多边形的内角和与外角和的度数比为3:2，那么这个多边形的边数为________
15. 解方程组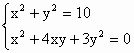
时，可将其化为两个方程组________________和________________。
16. 已知一组数据
，那么这组数据的标准差为________
17. 如图，在平面直角坐标系xOy中，点A（0，1），点B在x轴的正半轴上，
，在坐标轴上找一点P，使
为等腰三角形，那么符合条件的点P有________个。
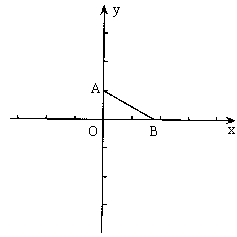
三、（共2小题，共11分）
18. （本小题满分6分）
当
时，求代数式
的值。
19. （本小题满分5分）
解方程：
四、（共2个小题，每小题5分，共10分）
20. 如图，已知测速站P和公路L在同一水平面上，P到公路L的距离PO为300米，事先在公路上找到了满足
的A、B两点安装测速设备。一辆汽车在公路L上沿AB方向匀速行驶，测得它从点A到点B所用的时间为9秒。
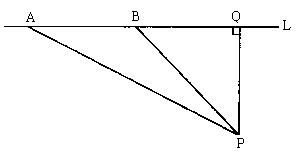
（1）计算此车从点A到点B的速度v为每秒多少米（结果精确到个位，
）；
（2）如果此路段限定时速不超过80千米，判断此车是否超速，并说明理由。
21. 已知：如图1，等腰梯形ABCD中，AD//BC，AB=DC，E为AB的中点，小明手头只有一把带刻度的直尺，他利用直尺上较长的刻度线画出了BC的垂线AF，垂足为F，（如图2），再连结EF。（如图3），然后他问同学小亮：“你知道EF和DC有什么位置关系吗？”
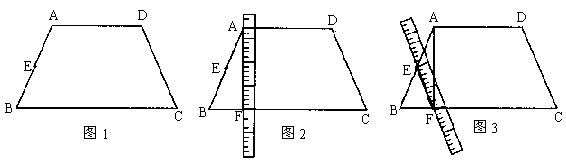
读完以上内容后，请解答下列问题：
（1）在图1中按小明的画法画出线段AF、EF；
（2）帮小亮证明EF和DC的位置关系。
五、（本题满分6分）
22. （1）观察下列等式：
①
②
③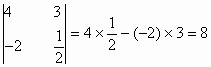
如果a、b、c、d为实数，那么以上三个等式中都使用了同一种运算
，可以看出，在这里，我们规定了
________
（2）在（1）中这种运算的规定下，回答下列问题：
①方程
可化为________________，它的解为________________
②现有一个关于x的方程
，用的形式可将其改写为________________。（不解方程）
六、（本题满分6分）
23. 为保护环境，某校环保小组成员收集废电池，小亮第一天收集了5节5号电池和12节7号电池，称得总重量264克；第二天收集了7节5号电池和6节7号电池，称得总重量为240克。
（1）5号电池和7号电池每节各重多少克？
（2）为估计六月份小组全体成员收集电池的总重量，该环保小组随机抽取了该月某5天小组全体成员收集废电池的情况。（如下表所示）
| 日期 | 5日 | 9日 | 12日 | 18日 | 24日 |
| 5号废电池（单位：节） | 29 | 30 | 32 | 28 | 31 |
| 7号废电池（单位：节） | 51 | 53 | 47 | 49 | 50 |
问：这5天，小组全体成员平均每天收集这两种废电池各多少节？估计六月份环保小组全体成员收集废电池的总重量是多少千克？
七、（本题满分7分）
24. 已知：正比例函数
和反比例函数
在同一坐标系中的图象有两个交点
，其中
（1）求k的取值范围；
（2）作
轴于点C，若
的面积为2，求该反比例函数的解析式。
八、（本题满分8分）
25. 已知：如图1，直线
交y轴于点C，点D（m，n）是这条直线上第一象限内的一点，以CD为直径的⊙M交x正半轴于
两点，交y轴于点E。
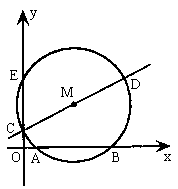
图1
（1）用m、n的代数式表示点E、M的坐标；
（2）求证：
（3）如图2，若抛物线
经过A、B、D三点，
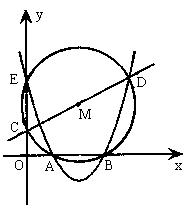
图2
①求a的值；
②当弦CE与弦AB的长度相等时，求抛物线的解析式。
九、（本题满分8分）
26. 已知：如图，
中，
，点P在AB边上由点A向点B匀速运动，点Q在CB边上由点C向点B匀速运动，它们同时出发，速度都为1厘米/秒，当点Q先到达B点时，点P也停止运动。设P、Q两点运动的时间为t秒。
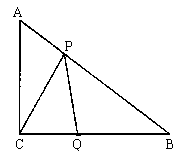
（1）若
的面积为s（
），求s（）与运动时间t（秒）的函数关系式及自变量t的取值范围；
（2）当为直角三角形时，它的面积是多少平方厘米？
（3）已知：P、Q两点的运动速度相同时，无论t为何值，都不可能是正三角形（请考试结束后进一步思考它的原因）。那么在“保持点P运动速度不变”的条件下，是否能通过改变点Q的运动速度，使在运动的过程中成为正三角形？若能，请求出点Q改变后的运动速度v和此时t的值；若不能，请说明理由。
【试题答案】
一、选择题（共12个小题，第1~4小题每题3分，第5~12小题每题4分，共44分）
1. D 2. A 3. B 4. D 5. C 6. B
7. A 8. B 9. B 10. D 11. C 12. C
二、填空题（共5个小题，每小题4分，共20分）
13. 
且
14.
5
15. 
16. 
17.
6
*第17题讲评说明：要使等腰
（1）以AB为底：作AB的中垂线交x轴于
，交y轴于
（2）以AB为腰：①要使A为顶角顶点：以A为圆心，AB为半径作圆，交x轴于
、B，交y轴于
②要使B为顶角顶点：以B为圆心，BA为半径作圆，交x轴于
，交y轴于A、
所以共有6个符合条件的点P：
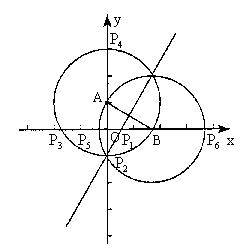
三、（共2个小题，共11分）
18. 解：
……2分
……3分
……5分
当时，原式
……6分
19. 解：设
，则原方程可化为
……1分
解得
……2分
当
时，
此方程无实数根 ……3分
当
时，
解得
……4分
经检验，都是原方程的根
所以原方程的根是……5分
四、（共2个小题，每小题5分，共10分）
20. 解：（1）在
中，
……1分
在
中，
……2分
……3分
（米/秒） ……4分
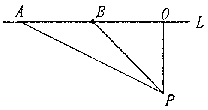
（2）
24米/秒＝86.4千米/时>80千米/时
（或80千米/时
米/秒<24米/秒）
该汽车超过了每小时80千米的限制速度 ……5分
21. （1）画图见图1
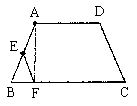
图1
（2）证明：梯形ABCD中，AD//BC，AB=DC
……2分
于F，E为AB的中点
为
斜边上的中线
……3分
……4分
……5分
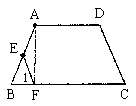
图2
五、（本题满分6分）
22. 解：（1）
……2分
（2）①
（或
）
……3分
……4分
②
……6分
*阅卷说明：第（2）②问中，其它符合题意的正确答案相应给分，如
等等。
六、（本题满分6分）
23. 解：（1）设5号电池每节重x克，7号电池每节重y克 ……1分
依题意得
……2分
解得
……3分
答：5号电池每节重24克，7号电池每节重12克。
（2）小组全体成员平均每天收集5号电池
（节）
……4分
平均每天收集7号电池
（节）
……5分
（克）
答：估计六月份环保小组全体成员收集废电池的总重量是39.6千克 ……6分
七、（本题满分7分）
24. 解：（1）
和在同一坐标系中的图象有两个交点A、B
两点的坐标是方程组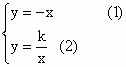
的解
……1分
消去y，整理得
（或
）
……2分
（或
）
……3分
*阅卷说明：由于本题条件特殊，也可根据和
图象所经过的象限及图象交点的个数直接判断出
。
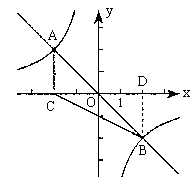
（2）由（1）得
，且……4分
异号
……5分
作
轴于点D
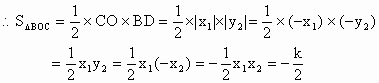
……6分
解得
，该反比例函数的解析式为
……7分
八、（本题满分8分）
25. （1）解：连结DE，作
轴于点G，
轴于点F，（如图1）
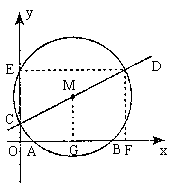
图1
为⊙M的直径
，即
轴
点E的坐标为（0，n） ……1分
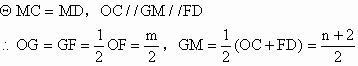
点M在第一象限
点M的坐标为
……2分
*阅卷说明：由点D在直线上得到
，利用此结论得到的点M坐标的其它正确表示相应给分，如点M的坐标还可表示为
或
等等。
（2）证明：
轴于点G，即
，M为圆心
……3分
，即
……4分
（3）①解一：设过A、B两点的抛物线的解析式为
抛物线过D点
把
代入上式，得
点D在第一象限
，两边除以n，得
……6分
解二：抛物线过A、B、D三点
由抛物线和圆有公共对称轴可知抛物线过E（0，n）点
当
时，
的两根为
又
……6分
②由①得抛物线的解析式为
解一：作于G，
于H（如图2）
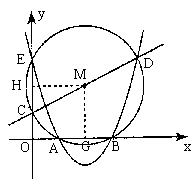
图2
，而点M在第一象限
点M的横、纵坐标相等，即
……7分
又点D在直线上
解由(1)、(2)组成的方程组，得
此时抛物线的解析式为
……8分
解二：
……7分
又点D（m，n）在直线上
方程(1)化为
两边平方，整理，得
解得
经检验，
是增根，
是方程(2)的解
点D在第一象限，
符合题意
抛物线的解析式为
……8分
*讲评说明：在第（3）问中注意以下两件事：
（1）以为根的一元二次方程（二次项系数为1）是
（见课本第29页）
（2）满足两个条件“经过
两点”的抛物线不确定。（如图3）
若设其解析式为
它的二次项系数不一定为1，需由第三个条件确定a的值，本题的第三个条件是“抛物线过D点”
图3
九、（本题满分8分）
26. 解：（1）
作
于D（如图1）
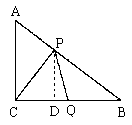
图1
则
，即
……1分
……2分
时，不存在；
时，P、Q的位置如图2所示
图2
的取值范围是
……3分
（2）
，即
，即Q点在D点右侧
又
，为直角三角形
只能
（如图3）
（见题后的“*讲评说明”）
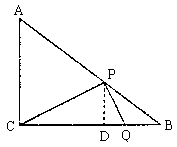
图3
此时
，即
直接开平方，得
（或整理，得
）
解得
……4分
由（1）得，此时
……5分
答：当为直角三角形时，它的面积为
（3）假设点Q运动的速度为v厘米/秒，P、Q两点运动t秒时，为正三角形
此时
仍成立，
，且
（如图4）
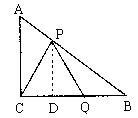
图4
（厘米/秒） ……6分
又
解得
……7分
点Q改变运动速度后，点P、Q运动到B点分别需要5秒和2.5秒，为使存在，需
，而
，在0与2.5之间
点Q改变后的运动速度为
厘米/秒，t为
秒时，能成为正三角形
……8分
*讲评说明：第（2）问中，应让学生养成分类讨论的意识和严谨的书写习惯，排除某种情况需写明原因，不能光心里知道不写在卷面上，如此题需排除
和
等于
的可能性，在分值富裕的情况下，这里会设一个得分点，就会有很多学生失分，需引起高度重视。