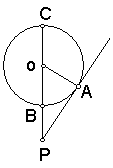冲刺试卷（三）
一、选择题
1、
的相反数是（ ）
A、 B、
C、
D、
2、计算
所得的结果是（ ）
A、 B、
C、
D、
3、方程
的根是（ ）
A、
，
B、
，
C、 D、
4、函数
中，自变量
的取值范围是（ ）
A、
B、
C、
且
D、
且
5、已知一元二次方程
的两根是
，
，则
的值是（ ）
A、 B、
C、
D、
6、一次函数
（
，
）的图象不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
7、样本
，，
，
，
，，，
的中位数和众数分别是（ ）
A、
， B、，
C、，
D、，
8、已知两圆的半径分别是，，圆心距是
，若两圆有公共点，则下列结论正确的是（ ）
|
B、
C、
D、
9、如图，半径为
的扇形
的中心角是
，
于点
，则图中阴影部分的面积为（ ）
A、
B、
C、
D、
|
，且较长的直角边在同一直线上，则图中的等腰三角形有（ ）
A、个 B、个
C、个 D、
个
11、某校计划，在校园内建造一座周长为米的花坛，同学们设计出正三角形、正方形和圆共三种图案，其中使花坛面积最大的图案是（ ）
A、正三角形 B、正方形 C、圆 D、不能确定
二、填空题（本题共有
小题，每小题，每小题分，共
分）
12、
的倒数是_______________。
13、写出经过点
的一个函数的解析式可以是__________。
14、下面是参加射击比赛预选赛的两名选手的十次命中的环数：甲，
，
，，，，，，，；乙，，，，，，，，，，你认为应该派______参加射击比赛。
15、抛物线
的顶点坐标为__________。
16、母线长为
，底面半径为
的圆柱的侧面积为________
。
17、若一个梯形内接于圆，有如下四个结论：①它是等腰梯形，②它是直角梯形，③它的对角线互相垂直，④它的对角互补，请写出正确正确结论的序号__________（把你认为正确的序号都填上）
|
（如图），
求作：的内切圆（说明：要求写出作法）
四、（本题共有小题，每小题分，共分）
19、先化简，再求值：
，其中
，
20、解方程：
五、（本题满分分）
21、已知二次函数
的图象如图所示
（1）求：这个二次函数的解析式和顶点的坐标
（2）设抛物线与
轴交于点
，求：四边形
的面积。
六、（本题满分分）
22、如图，
切
于
，割线
，经过圆心
，（1）若
，
，求的半径。（2）在上是否存在一点，使
成立？为什么？
|
七、（本题满分
分）
23、某厂工业废气年排放量为
万立方米，为改善大气环境质量，决定分二期投入治理，使废气的年排放量减少的百分率相同，（1）求每期减少的百分率是多少？（2）预计第一期治理中梅减少万立方米废气需投入万元，第二期治理每减少万立方米废气需投入
万元，问两期治理完成后需要投入多少万元？
|
是边长为的正方形的边
上一个动点，设
，四边形
的面积为，求与之间的函数关系式，并指出自变量的取值范围。
九、（本题满分
分）
|
中，
，
，为
上一动点，
的形状可由
的长来确定
（1）若为直角三角形，求的长；
（2）若为锐角三角形，求的取值范围；
（3）若为钝角三角形，求的取值范围。