初三数学总复习教案（一）
一元一次方程
知识结构
等式与方程 等式性质
方程 
一次方程的解法：去分母、去括号、移项、合并同类项、系数化为1
目标要求
1． 了解等式和方程的相关概念，掌握等式性质，会对方程的解进行检验．
2． 灵活运用等式性质和移项法则解一元一次方程．
【典型例析】
例1 （2000 湖北十堰）解方程
时，去分母后正确的结果是（ ）.
A． 4x+1－10x+1=1 B．4x+2－10x－1 =1
C．4x+2―10x―1＝6 D．4x+2－10x+1=6
【特色】此题设计旨在考查学生对于解一元一次方程的去分母、去括号等步骤的理解.
【解答】去分母是根据等式性质，方程两边同乘以６.
去分母，得 
2(2x+1)-(10x+1)=6.
去括号，得 4x+2―10x―1=6. 选 C
【拓展】用去分母解方程时 , 根据等式性质,方程两边同乘最简公分母这一步不要省略.
例2（2001年 泰州） 解方程：（0.1x-0.2）/0.02－（x+1）/0.5＝3
分析：利用解一元一次方程方法和步骤完成本题。
解：（0.1x-0.2）/0.02-（x+1）/0.5=3
去分母，得5x-10-2(x+1)=3，去括号得 5x-10-2x-2=3
移项，合并同类项，得3x=15
系数化为1，得x=5
例3 （2002年 宁夏） 某乡中学现有学生500人,计划一年后女生在校生增加3%，男生在校生增加4%，这样，在校学生将增加3.6%，那么该学校现有女生和男生人数分别是（ ）
（A）200和300 (B)300和200 （C）320和180 （D）180和320
分析：可列一元一次方程或列二元一次方程组：
解法一：设该校有女生x人，则男生有（500-x）人，
依题意有：x（1+3%）+（500－x）（1+4%）＝500（1+3.6%）
1.03x+500×1.04-1.04x＝500×1.036
-0.01x＝-2
x＝200
则500-x＝500-200＝300
因此女生有200人，男生有300人，∴选（A）
解法二：设该校有女生x人，男生有y人
x+y=500
依题意有
x(1+3%)+y(1+4%)=500(1+3.6%)
x=200
解之有
y=300
∴该校有女生200人，男生有300人，故选（A）
课堂练习：
1、
若
与
互为相反数，求
。
2、
若
是关于的一元一次方程，求
的值。
3、
求方程
在自然数范围内的解。
4、
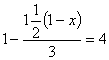
5、（03海淀）某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元。
（1）求该同学看中的随身听和书包单价各是多少元？
（2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），但他只带了400元钱，如果他只在一家超市购买看中的这两样物品，你能说明他可以选择哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？