2004年新疆维吾尔自治区初中毕业与升学考试试卷
数学
考生须知：1. 本试卷满分120分.考试时间120分钟.
2. 答题前，考生应先在密封区内，认真填写准考证号、姓名、县（市）和学校.
一、选择题（每小题4分，共32分）
每题四个选项中，只有一个是正确的，请将选项前的字母符号填入下表相应表
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 选项 |
格内.
1. 
的平方根是
A．
B．9
C．
D．3
2.
用换元法解方程：
，设
，则原方程可变形为
A．
B．
C．
D．
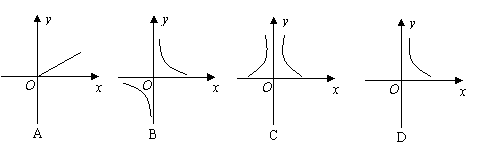
3. 三角形的面积为8cm2，这时底边上的高ycm与底边xcm间的函数关系的图象大致是
 |
4. 对“五·一”黄金周7天假期去天池景区旅游的人数进行统计，每天上山旅游的人数统计如下表：
| 日期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 | 5月6日 | 5月7日 |
| 人数（单位：万） | 1.2 | 2 | 2.5 | 2 | 1.2 | 2 | 0.6 |
其中众数和中位数分别是
A．1.2，2
B．2，2.5 C．2，2
D．1.2，2.5
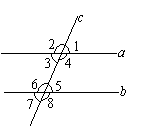
5. 如图，直线a//b，如下结论正确的是
A．
B．
C．
D．
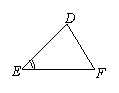
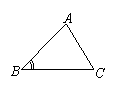
6. 下列各组条件中，能判定△ABC≌△DEF的是
A．AB=DE，BC=EF，∠A=∠D
B．∠A=∠D，∠C=∠F，AC=EF
C．AB=DE，BC=EF，△ABC的周长= △DEF的周长
D．∠A=∠D，∠B=∠E，∠C=∠F
7.
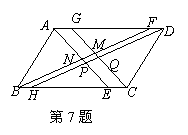
如图，
中，四个内角的平分线交于M、N、P、Q点，则四边形MNPQ是
A．矩形 B．正方形 C．菱形 D．平行四边形
 | |||
 | |||
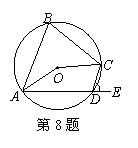
8. 如图，四边形ABCD内接于⊙O，E是AD延长线上一点，若∠AOC=140°，则∠EDC的度是
A．40° B．70° C．80° D．65°
二、填空（每小题4分，共20分）
9. 已知
，则
.
10.
当
时，方程
的两根之差是7.
11.
一弓形弦长为
cm，弓形所在圆的半径为7cm，则弓形高是
.
12.
等腰梯形的腰长为6，底角的正切值为
，下底长为
，则上底长为
.
13.
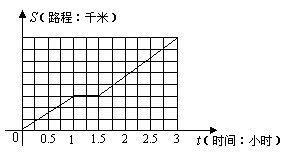下图是一个路程随时间变化的图象，请你根据图所提供的信息，结合自己的实际写出一个生活片断.（你可以在S轴上标出一些数据）
 |
三、解答题（共9题，满分68分）
14. （5分）用若干辆载重量为8吨的汽车运一批货物，若每辆汽车只装5吨，则剩下10吨货物，若每辆车装满8吨，则最后一辆汽车不空也不满，请问有多少辆汽车？
15. （5分）阅读并解答
对于一元二次方程
，通过配方可将方程变形为：
. 完成下列填空：
（1）方程的根的情况取决于
的值的符号.
（2）某同学判断关系x的方程
的根的情况，解答如下：
解：
1
2
3
4
原方程无实数根.
5
请你判断他的解答是否正确，并写明你的判断理由.
16. （7分）在一张长12cm、宽5cm的矩形纸片内，要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH（见方案一），张丰同学沿矩形的对角线AC折出∠CAE=∠DAC，∠ACF=∠ACB的方法得到菱形AECF（见方案二），请你通过计算，比较李颖同学和张丰同学的折法中，哪种菱形面积较大？
 |
17.
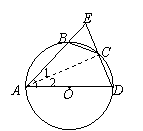
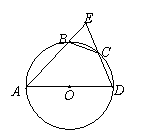（5分）如图，四边形ABCD内接于⊙O，并且AD是⊙O的直径，C是
的中点，AB和DC的延长线交⊙O外一点E.求证：BC=EC.
18. （8分）新疆某地为了治理土地沙化趋势，计划2000年~2004年造林种草面积逐年增加，每年年底累计完成造林种草总面积如下表：
| 年度 | 1999年 | 2000年 | 2001年 | 2002年 | 2003年 | 2004年 |
| 造林种草面积 （单位：千米2） | 7 | 8 | 10 | 13 | 17 | 21 |
（1）画出2000年~2004年每年完成造林种草面积的频率分布直方图（或条形统计图）.
 |
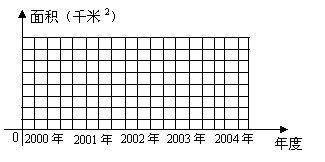（2）若取从2000年~2004年每年完成造林种草面积的中位数为每年增加值，到2010年底该地应累计完成造林种草面积多少？
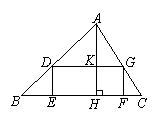
19. （6分）如图，在△ABC中，点E、F在BC上，点D、G分别在AB、AC边上，四边
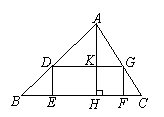形DEFG是矩形，若矩形DEFG面积与△ADG的面积相等，设△ABC的BC边上高AH与DG相交于点K.
求
的值.
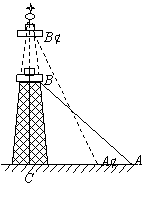20. （8分）原电视发射塔为BC.为稳固塔身，周围拉有钢丝地锚线（如图线段AB），若AB=60m，并且AB与地面成45°角，欲升高发射塔的高度到
，同时原地锚线仍使用，若塔升高后使地锚线与地面成60°角，求电视发射塔升高了多少米？（即
的高度）（精确到0.01m）.
21.
（12分）（适用人教版教材的地区做）
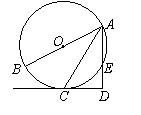
如图，AB是⊙O的直径，CD切⊙O于C点.AD交于⊙O点E.
（1）探索AC满足什么条件时，有AD⊥CD，并加以证明.
（2）当AD⊥CD，AD=4，AB=5时，求AC、DE的长度.
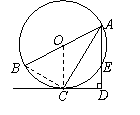
22. （12分）（适用华东版教材的地区做）
如图1，AD是⊙O的直径，BC切⊙O于点D，AB、AC
交⊙O于点E、F.
（1）试探索线段AE、AB、AF、AC有什么等量关系并加以证明.
（2）如果将直线BC向上平移，使BC仍于AD垂直，如图2，AE、AB、AF、AC有什么等量关系，请写出这个等量关系.
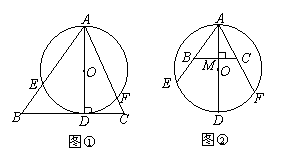
23. （12分）若二次函数的图象的对称轴方程是
，并且图象过A（0，-4）和B（4，0）.
（1）求此二次函数图象上点A关于对称轴对称的点
的坐标.
（2）求此二次函数的解析式.
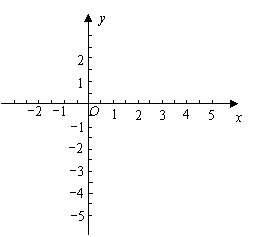（3）画出这个二次函数的图象.
2004年新疆维吾尔自治区初中毕业升学考试试卷
数学参考答案及评分标准
说明：
1 参考答案供阅卷教师参考，学生答题时，只要解题思路方法正确，答案符合题意，虽与参考答案有出入，均可给分.
2 本试卷中的开放性题目，由于答案不唯一，学生答案符合题意的，同样给分.
一、选择题（每小题4分，共32分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | B | D | C | A | C | A | B |
二、填空题（每小题4分，共20分）
9.20；10.
； 11. 2cm或12cm；12.
；13.(只要符合图形和生活实际情况都给分)三、解答题（共9题，满分68分）
14. 设有x辆汽车 ……………………………………………………………………………1分
则
………………………………………………………………2分
解之得：1
2 
∴不等式组解集为
…………………………………………………………3分
∴满足不等式组解集的整数解为4或5………………………………………………4分
答：有4辆或5辆汽车.………………………………………………………………5分
15. 解：（1）b2-4ac …………………………………………………………………………1分
（2）有错，错在第3步……………………………………………………………2分
理由如下：
当k>0时，-16k<0方程没有实数根………………………………………………3分
当k=0时，-16k=0方程有两个相等实数根………………………………………4分
当k<0时，-16k>0方程有两个不相等实数根……………………………………5分
16. 解：（方案一）
……………………………………………………………………2分
（方案二）
设BE=x，则CE=12-x ………………………………………………………………3分
由AECF是菱形，则AE2=CE2
………………………………………………………………5分
…………………………………………………………6分
比较可知，方案二张丰同学所折的菱形面积较大. ………………………7分
17. 证明：连结AC ……………………………………………………………………1分
∵AD是⊙O的直径
∴∠ACD=90°=∠ACE ……………………………………………………………2分
∵
四边形ABCD内接于⊙O
∴∠EBC=∠D ……………………………3分
是的中点
………………………………………………………………………4分
∴∠EBC=∠E
∴BC=EC …………………………………………………………………………5分
18. 解：（1）由1999年至2004年底累计造林种草总面积可得：
2000年、2001年、2002年、2003年、2004年各年度完成造林种草面积分别
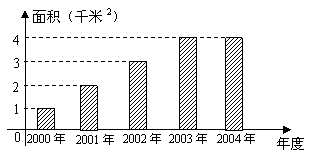为：1万千米2、2万千米2、3万千米2、4万千米2、4万千米2……2分
………………4分（画图2分）
（2）由2000年~2004年度每年完成造林种草面积为（单位：千米2）
1，2，3，4，4……………………………………………………………5分
中位数：3…………………………………………………………………6分
到2010年底累计造林种草面积=21+6×3
=21+18=39（千米2） …………8分
19. 解：
…………………………1分
……………2分
由题意得：
………3分
………………………………………………………………………4分
即
………………………………………………………………………5分
由DG//BC可得△ADG∽△ABC，得
…………………………6分
20. 解：在Rt△ACB中
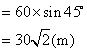…………………………3分
在Rt△
中
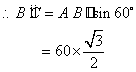
…………………………………………………………………6分
∴电视塔升高的高度：
…………………………………………8分
21.（人教版教材）
解：（1）当AC平分∠BAD时，有AD⊥CD………………………………………………2分
连结OC，由CD是⊙O的切线，必有OC⊥CD
若AD⊥CD成立，则OC//AD……………………………………………………3分
得∠OCA=∠DAC …………………………………………………………………4分
又∵⊙O中，∠OCA=∠OAC
∴∠OAC=∠DAC
即：AC平分∠BAD ………………………………………………………………5分
[说明]以上证明是执果索因.也可由AC平分∠BAD推证出AD⊥CD，评分标准参考以上.
（2）连结BC ……………………………6分
由1可得AC平分∠BAD
则∠BAC=∠CAD，∠BCA=∠CDA=Rt∠
∴△ACB∽△ADC……………………7分
…………………………8分
…………………………………………………………………………9分
……………………………………………10分
由切割线定理：
及AD=4解得DE=1 …………………12分
22. （华东版教材）
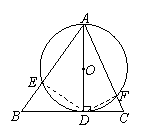
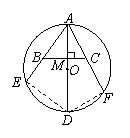结论：线段AE、AB、AF、AC之间等量关系是：
…………………2分
证明：（1）连结DE、DF …………………3分
在⊙O中中
∵AD是⊙O的直径
∴∠AED=∠AFD=90° ……………4分
又∵BC是⊙O的切线
∴∠ADC=∠ADB=90°，∠BAD=∠DAE …………………………………5分
∴△ADB∽△AED………………………………………………………………6分
……………………………………………………………………7分
1 ………………………………………………………8分
同理：△ADC∽△AFD
2 ………………………………………………………9分
由12可得： ……………………………………………10分
（2）答：若将直线BC向上平移，使CD仍与AD垂直，AE、AB、AF、AC仍有（1）中的等量关系. …………………………………………………………………………12分
23. 解：1设
点
和点关于对称
……………………………………………………2分
………………………………………………………………………3分
点坐标（3，-4）………………………………………………………4分
2设二次函数解析式
……………………………………5分
把和
代入可得
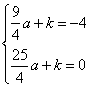………………………………………………………………7分
解得：
………………………………………………………8分
∴此二次函数的解析式为
即：
…………………………………………………………9分
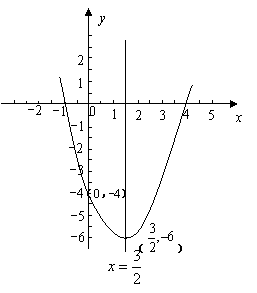3
…………12分（图形