初三数学2004中考专题跟踪练习（解直角三角形）
一、填空题
1.
求值：
+2sin30°－tan60°＋cot45=__2－
________。:
2.
（广东03/6）若∠A是锐角，cosA＝
，则∠A＝ 30° 。
3.
（陕西03/12）在△ABC中，∠C＝90°，若tanA＝
，则sinA＝ 
；
 | |||
 | |||
4. （黑龙江03/10）如图：某同学用一个有60°角的直角三角板估测学校旗杆AB的高度，他将60°角的直角边水平放在1.5米高的支架CD上，三角板的斜边与旗杆的顶点在同一直线上，他又量得D、B的距离为5米，则旗杆AB的高度约为 10 米。（精确到1米，
取1.732）
5. （上海闵行区03/14）已知等腰三角形的周长为20，某一内角的余弦值为
，那么该等腰三角形的腰长等于 6或
。
6. （四川03/3）如图，△ABC中，AD⊥BC于D，CE⊥AB于E，且BE＝2AE，已知AD＝
，
tan∠BCE＝
，那么CE＝ 
。
7. （上海03/13）正方形ABCD的边长为1。如果将线段BD绕着点B旋转后，点D落在BC延长线上的点
处，那么tan∠BA＝ 
。
8. （宁夏03/19）在倾斜角为30°的山坡上种树，要求相邻两棵树间的水平距离为3米，那么，相邻两棵树间的斜坡距离为 
米。
二、选择题
1. （四川03/8）在△ABC中，已知AC＝3、BC＝4、AB＝5，那么下列结论成立的是（ B ）
A、SinA＝
B、cosA＝
C、tanA＝
D、cotA＝
2.
（黄冈03/9）在△ABC中，AB＝AC＝3，BC＝2，则6cosB等于
（ B ）（A）3
（B）2
（C）
（D） 
3. 
（扬州03/11）为测楼房
的高，在距楼房
米的
处，测得楼顶
的仰角为
,则楼房
的高为（ A ）
A．
米 B．
米 C．
米 D．
米
4.
（烟台03/10）从边长为1的等边三角形内一点分别向三边作垂线，三条垂线段长的和为（ A ）（A） （B） （C）
（D）
12、（重庆03/11）如图：在等腰直角三角形ABC中，∠C＝90°，AC＝6，D是AC上一点，若tan ∠DBA＝
，则AD的长为（
B
） A、 B、2
C、1 D、2
13、（重庆03/8）已知：如图，梯形ABCD中，AD∥BC，∠B＝45°，∠C＝120°，AB＝8，则CD的长为（ A ） A、
B、
C、
D、
三、解答题
1.
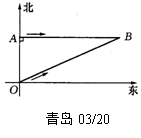（青岛03/20）（6分）人民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只，正以24海里／小时的速度向正东方向航行．为迅速实施检查，巡逻艇调整好航向，以26海里／小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问⑴需要几小时才能追上？（点B为追上时的位置）⑵确定巡逻艇的追赶方向（精确到0．1°）．
参考数据：sin66．8°≈ 0．9191 cos 66．8°≈ 0．393
sin67．4°≈ 0．9231 cos 67．4°≈ 0．3846
sin68．4°≈ 0．9298 cos 68．4°≈ 0．368l
sin70．6°≈ 0．9432 cos70．6°≈ 0．3322
2.
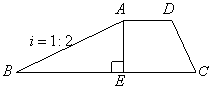如图，沿江堤坝的横断面是梯形ABCD，坝顶AD=4m，坝高AE=6 m，斜坡AB的坡比
，∠C=60°，求斜坡AB、CD的长。
解：∵斜坡AB的坡比，
∵AE：BE=
，又AE=6 m
∴BE=12 m
∴AB=
（m）
作DF⊥BC于F，则得矩形AEFD，有DF=AE=6 m，∵∠C=60° ∴CD=DF·sin60°= m
答：斜坡AB、CD的长分别是
m ，
m。
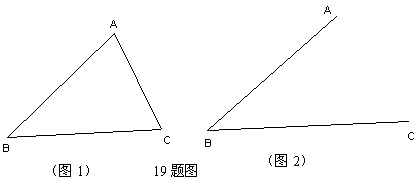
3. （荆门03/19）（本题满分8分）（1）如图1，在△ABC 中，∠B 、∠C
均为锐角，其对边分别为b、c,求证：
=
；
（2）在△ABC
中，AB=，AC=，∠B
=450,问满足这样的△ABC
有几个?在图2中作出来(不写作法,不述理由)并利用(1)的结论求出∠ACB的大小。
4.
2003资阳市如图，在△ABC中，已知∠ACB＝90°，CD⊥AB于D，AC＝
，BD＝3。
（1）请根据下面求cosA的解答过程，在横线上填上适当的结论，使解答正确完整：
∵CD⊥AB ∠ACB＝90°
∴AC＝ AB cosA， AD ＝AC·cosA
由已知AC＝，BD＝3
∴＝AB cosA＝（AD＋BD）cosA＝（cosA＋3）cosA
设
＝cosA，则
＞0，且上式可化为
＋－＝0，则此解得cosA＝＝
（2）求BC的长及△ABC的面积。
（2）解：在Rt△ABC中，BC=AC·tanA=·
＝6
S△ABC=
5. （安徽03/21）如图是五角星，已知AC＝a，求五角星外接圆的直径（结果用含三角函数的式子表示）。
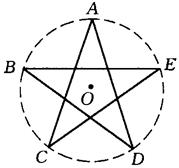
【解】
